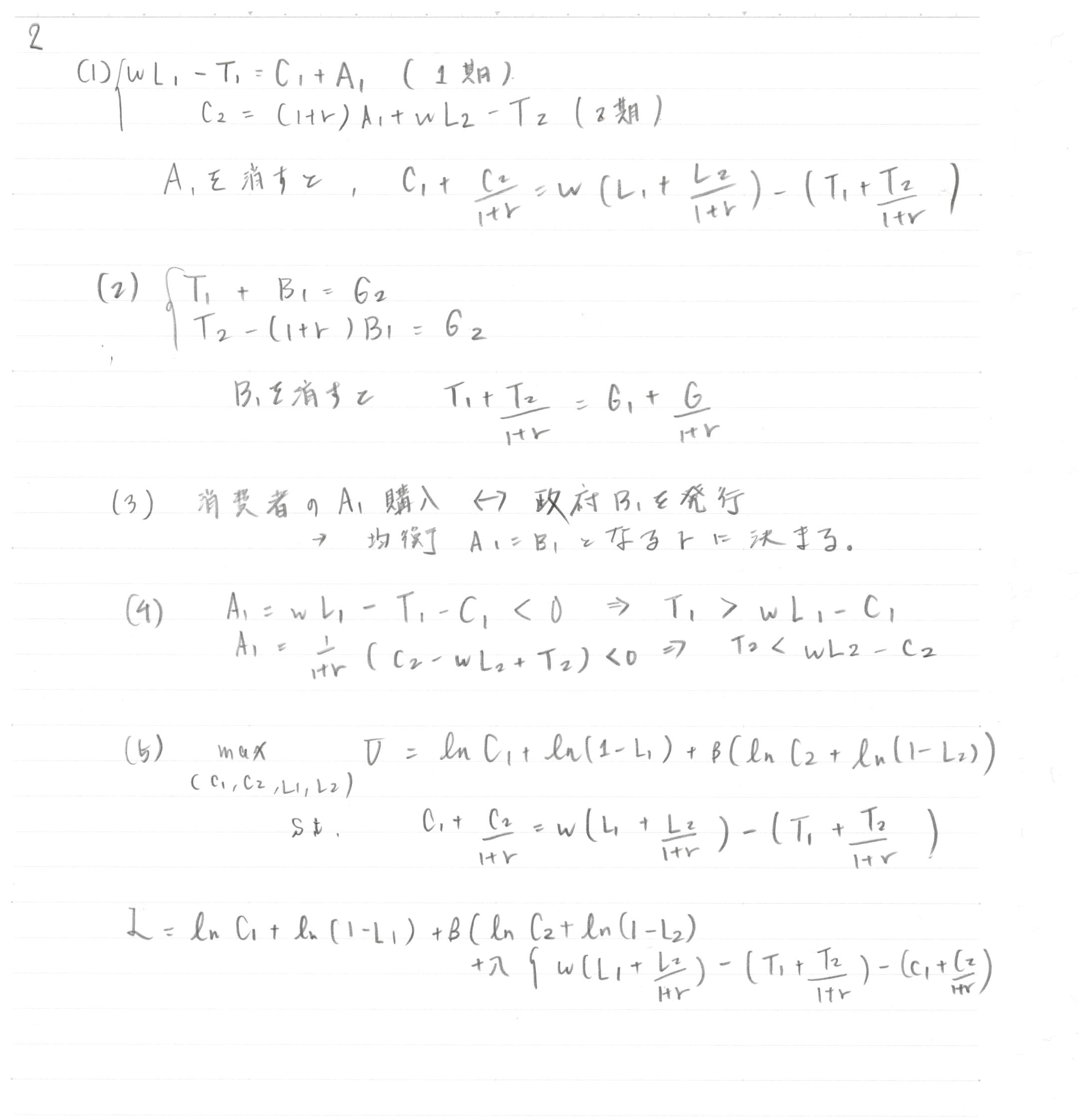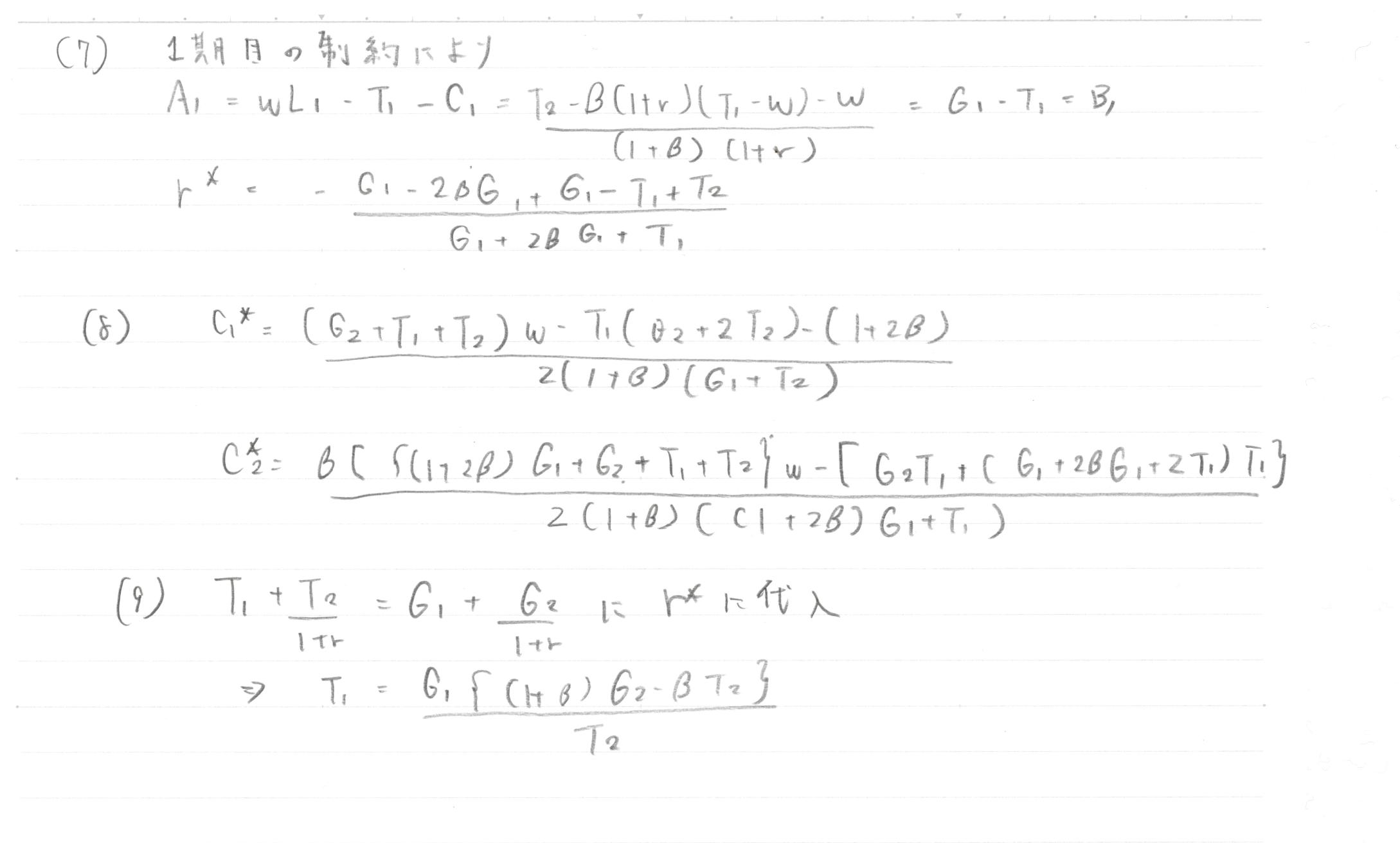*京都大学大学院経済学研究科では2023年実施(2024年度入学)の筆記は行わず、書類・面接選考になっております。
通常の成績、研究計画書、面接対策を中心に行いましょう。
2020年度(2019年実施)【経済理論】
第1問(ミクロ経済学)
問題1
問1
シェパードの補題を用いて導きます。
\begin{equation}
\begin{aligned}
h_{1}\left(P_{1}, P_{2}, u\right) & =\frac{\partial e\left(P_{1}, P_{2}, u\right)}{\partial P_{1}} \\
& =\frac{3}{4} u^{\frac{1}{4}}\left(\frac{P_{1}}{P_{2}}\right)^{-\frac{1}{4}}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
h_{2}\left(P_{1}, P_{2}, u\right) & =\frac{\partial e\left(P_{1}, P_{2}, u\right)}{\partial P_{2}} \\
& =\frac{1}{4} u^{1 / 4}\left(\frac{P_{1}}{P_{2}}\right)^{3 / 4}
\end{aligned}
\end{equation}
(2)
\( h_{1}とh_{2} \)から\( \frac{P_{1}}{P_{2}} \)を消します。
\begin{equation}
\begin{array}{l}
\max _{\left(x_{1}, x_{2}\right)} u=\frac{256}{27} x_{1}^{3} x_{2} \\
\text { s.t. : } p_{1} x_{1}+P_{2} x_{2}=y
\end{array}
\end{equation}
また,\( MRS_{12}\)と需要関数\( x_{1}, x_{2}\)は
\begin{equation}
M R S_{12}=3 \frac{x_{2}}{x_{1}}=\frac{p_{1}}{p_{2}}
\end{equation}
\begin{equation}
\begin{array}{l}
x_{1}=\frac{3 y}{4 P_{1}} \\
x_{2}=\frac{z_{2}}{4 P_{2}}
\end{array}
\end{equation}
\( u\)に代入し間接効用関数を求めます。
\begin{equation}
\begin{aligned}
v\left(P_{1}, P_{2}, y\right) & =\frac{256}{27}\left(\frac{3 y}{4 P_{1}}\right)^{3}\left(\frac{y}{4 P_{2}}\right) \\
& =\frac{y^{4}}{P_{1}^{3} P_{2}}
\end{aligned}
\end{equation}
問2
(1)
ロイの恒等式より
\begin{equation}
x_{i}^{*}=-\frac{\frac{\partial v}{\partial P_{i}}}{\frac{\partial v}{\partial y}} \Rightarrow\left\{\begin{array}{l}
x_{1}^{*}=\frac{3 y}{4 P_{1}} \\
x_{2}^{*}=\frac{y}{4 P_{2}}
\end{array}\right.
\end{equation}
となり、問1の(2)と同じになります。
(2)
間接効用関数を\( y\)で解きます.それによって,支出関数を導けます.
\begin{equation}
v=\frac{y^{4}}{P_{1}^{3} P_{2}} \Rightarrow \begin{array}{l}
y^{4}=P_{1}^{3} P_{2} v
y=P_{1}^{3 / 4} P_{2}^{1 / 4} v^{1 / 4}
\end{array}
\end{equation}
\begin{equation}
e\left(P_{1}, P_{2}, u\right)=u^{1 / 4} P_{1}^{3 / 4} P_{2}^{1 / 4}
\end{equation}
問題2
価格をp,需要量をy,と表すと,以下の条件
$p>0$,かつ,$10>3y>0$,が成立し,市場の逆需要関数は以下によって与えられると仮定しましょう。
市場には2つの企業,企業1と企業2,が存在し,それぞれの企業の供給量を$y_1$,$y_2$とおくと,以下の条件
$y=y_1+y_2$,が成立し,企業1と企業2の費用関数を,それぞれ,$C_1=C_1(y_1)$と$C_2=C_2(y_2)$は以下によって与えられると,と仮定します。
$C_1(y_1)=2y_1$,かつ,$C_2(y_2)=2y_2$
問1
$y_1(0,\frac{8}{3})$および,$y_2(0,\frac{8}{3})$を仮定します。この複占モデル,企業1と企業2の反応関数をそれぞれ$R_1=R_1(y_1)$とおく。企業1と企業2の反応関数$R_1:(0,\frac{8}{3})$Rと$R_2:(0,\frac{8}{3})$Rを求めましょう。
複占モデルでは,各企業は自身の供給量を決定することによって利益を最大化するため,費用関数と逆需要関数から反応関数を求めます。
逆需要関数: $p=10-3y$
企業1の利益関数: $\pi_1 = p\cdot y_1 – C_1(y_1) = (10-3y)\cdot y_1 – 2y_1$
同様に,
企業2の利益関数: $\pi_2 = p\cdot y_2 – C_2(y_2) = (10-3y)\cdot y_2 – 2y_2$
企業1と企業2の供給量$y_1$と$y_2$を決定するためには,以下の2つの条件が成立する必要があります。 利益が最大化されていること: $\frac{\partial \pi_1}{\partial y_1}=0$かつ,$\frac{\partial \pi_2}{\partial y_2}=0$ 供給量が需要量に等しいこと: $y_1+y_2=y$ 上記2つの条件から, $y_1$と$y_2$を求め,反応関数$R_1$と$R_2$を導出することができます。
$R_1: y_1=\frac{\frac{\partial \pi_1}{\partial p}}{\frac{\partial \pi_1}{\partial y_1}}$ $R_2: y_2=\frac{\frac{\partial \pi_2}{\partial p}}{\frac{\partial \pi_2}{\partial y_2}}$
ここで求めた$R_1$と$R_2$が企業1と企業2の反応関数です。
問2
この複占モデルの,クールノー均衡おける,企業1および企業2の産出水準をそれぞれ$y_1^*$,$y_2^*$と置きます。問1で求めた反応関数$R_1=R_1(y_2)$と$R_2=R_2(y_2)1$をもちいて,クールノー均衡($y_1^*,y_2^*$)を求めましょう。
クールノー均衡を求めるには、企業1、2が自分の投入量を増やしたときに得られる利益増加を最大化することを考えます。すなわち、企業1、2の「反応関数」を求め、それぞれ最大化することを考えます。
問題文より,利益関数は $\pi_1 = p\cdot y_1 – C_1(y_1) = (10-3(y_1+y_2))\cdot y_1 – 2y_1$ となるので,企業1の反応関数は$y_2 = R_1(y_2)=\frac{8}{3} – \frac{3}{3}y_1 $となる.同様に,企業2の反応関数は$y_1= R_2(y_1)=\frac{8}{3} – \frac{3}{3}y_2 $となります。
クールノー均衡では,$R_1=R_1(y_2)$が成り立つので,
問3. 企業1が先導者, 企業 2 が追随者,として振る舞うシュタッケルベルク型複占モデルを考える. 企業の利潤関数を $\pi_1$ =$\pi_1(y_1)$ とおく. 問1で求めた企業 2 の反応関数 $R2=R2(y1)$ をもちいて, 企業 1 の利潤関数 $\pi_1: (0,\frac{8}{3}) $→ R を求めよ。
シュタッケルベルク型複占モデルを考える時の利潤関数を求めるには,先導者の利潤関数に追随者の反応関数を代入することで導出することができます.
\[
\begin{aligned}
\pi _{1}=\left\{ 10-3\times \left( y_{1}+\dfrac{8-3y_{1}}{6}\right) \right\} y_{1}-2y_{1}\\ =4y_{1}-\dfrac{3}{2}y^{2}
\end{aligned}
\]
問4. 企業1が先導者, 企業2 が追随者,として振る舞うシュタッケルベルク型複占モデルの シュ タッケルベルク均衡における, 企業1および企業 2 の産出水準をそれぞれ および とおく. 間 3で求めた 企業1 の利潤関数 $\pi_1$ =$\pi_1(y_1)$ 問1で求めた企業2 の反応関数 $R2=R2(y1) $をもちいて,シュタッケルベルク均衡(3) を求める。
シュタッケルベルク均衡を求めるには,先導者の利潤関数に追随者の反応関数を代入して微分することで求めることができます。
\[
\begin{aligned}\dfrac{\partial \pi _{1}}{\partial y_{1}}=4-3y_{1}=0\\
\left( y_{1}^{L},y_{2}^{F}\right) =\left( \dfrac{4}{3},\dfrac{2}{3}\right) \end{aligned}
\]
第2問(マクロ経済学)
1
(1)
(2),(3),(4)
2
(1),(2),(3),(4),(5〜)
(〜5),(6)
(7),(8),(9)