問題2
(1)均衡では,労働供給量$L^s=w$と労働需要量Lが等しくなることを利用します.問題の設定より,企業の利潤$\pi$は,
\begin{align}
\pi = L-\frac{1}{2}L^2-wL = L-\frac{1}{2}L^2-L^2\quad\quad(4)
\end{align}
となります.利潤最大化の一階条件より,
\begin{align}
\frac{\partial \pi}{\partial L} = 1-L-2L=0 \Leftrightarrow L=\frac{1}{3}\quad\quad(5)
\end{align}
となります.よって,均衡における雇用量と賃金は,共に$\frac{1}{3}$です.
\begin{align}
\pi = L-\frac{1}{2}L^2-wL = L-\frac{1}{2}L^2-L^2\quad\quad(4)
\end{align}
となります.利潤最大化の一階条件より,
\begin{align}
\frac{\partial \pi}{\partial L} = 1-L-2L=0 \Leftrightarrow L=\frac{1}{3}\quad\quad(5)
\end{align}
となります.よって,均衡における雇用量と賃金は,共に$\frac{1}{3}$です.
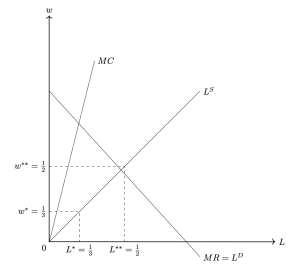
(2)考えている労働市場では買い手独占なので,企業は労働需要関数を限界収入曲線として考えることができます.つまり,
\begin{align}
L^D = MR = \frac{d(L-\frac{1}{2}L^2)}{dL}=1-L\quad\quad(6)
\end{align}
となる.また,限界費用MCは,
\begin{align}
MC = \frac{dC}{dL}=\frac{dL^2}{dL}=2L\quad\quad(7)
\end{align}となる.これらを,横軸に労働投入量,縦軸に賃金をとって作図してみると,
となります.このとき,$L^{**}$までは失業を生むことなく,(1)で求めた水準よりも雇用を増やすことができます.この点は,
\begin{align}
L^S = L^D \Leftrightarrow L = 1-L \Leftrightarrow L=\frac{1}{2}\quad\quad(8)
\end{align}
となります.よって,失業を生むことなく,(1)で求めた水準よりも雇用を増やすことができる賃金の範囲は,
\begin{align}
\frac{1}{3} < w \leq \frac{1}{2}\quad\quad(9)
\end{align}
となります.