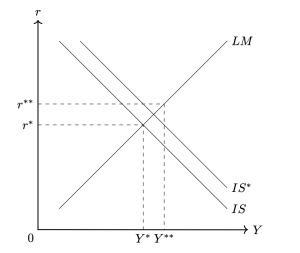
(3)政府支出増大の効果を図などを用いて説明です.
IS曲線とLM曲線より,財市場と貨幣市場が同時均衡は,
\begin{align*}
\frac{(a-1)Y+b+G}{c} &= \frac{dY-M}{e}\\
(\frac{a-1}{c}-\frac{d}{e})Y&=-(\frac{M}{e}+\frac{b+G}{c})\\
Y &= \frac{-(\frac{M}{e}+\frac{b+G}{c})}{(\frac{a-1}{c}-\frac{d}{e})}\\
&= \frac{-cM-e(b+G)}{e(a-1)-cd}
\end{align*}
\frac{(a-1)Y+b+G}{c} &= \frac{dY-M}{e}\\
(\frac{a-1}{c}-\frac{d}{e})Y&=-(\frac{M}{e}+\frac{b+G}{c})\\
Y &= \frac{-(\frac{M}{e}+\frac{b+G}{c})}{(\frac{a-1}{c}-\frac{d}{e})}\\
&= \frac{-cM-e(b+G)}{e(a-1)-cd}
\end{align*}
となります.このとき,$\frac{dY}{dG}=-\frac{e}{e(a-1)-cd}>0$より,
所得は増加します.また,Gの増加によってIS曲線のみがシフトします.これを図示すると,
よって,均衡では所得Y,実質利子率rの両方が増加します.