1. はじめに
本稿では、製造業者(manufacturer)と小売(retailer)の垂直的な関係を分析するフレームワークを提供します。ここで、製造業者を上流企業(upstream firm)、小売を下流企業(downstream firm, or industrial consumer)とも呼びます。
消費者にとっては、小売から財を購入し、消費するだけですが、通常の市場とは異なり、企業間の垂直的な関係があることからさまざまな問題(社会的に望ましくない結果)が発生します。
また、下流企業の意思決定は、直接的に上流企業の利潤に影響を与えることから、上流企業は下流企業をコントロールするインセンティブがあり、これをVertical Controlと言います。上流企業が下流企業を統合した場合の利潤を、vertical integrated profitと呼び、これは独占利潤に等しくなります。
異なる企業間の垂直的関係を分析することは、競争政策の観点からも、ビジネス上での意思決定を考える上でも重要です。以下では、Tirole(1988)、石橋(2021)に沿ってその概観を提供します。
2. 線形価格 vs 垂直的取引
2.1 モデルの設定
ここでは、以下のような市場を考えます。
・ 製造業者は1社(すなわち、monopolist)で、限界費用cで中間財(intermediate good)を生産
・ 製造業者は、中間財を小売に販売
・ 小売は製造業者から中間財を受け取った後、中間財を最終財に(場合によっては加工して)変形する
・ 小売は最終財を消費者に販売(販売費用は0とする)
・ $p_w$を卸売価格(wholesale price)とする。つまり、中間財の価格
・ $p$を最終財価格とする
・ $q$を小売によって購入される中間財の量とする
・ 小売は仕入れた中間財を全て消費者に販売すると仮定
・ $q = D(p)$を右下がりの需要関数とする
ここで、線形価格(linear price)とは、小売が製造業者から財を購入する際の価格体系であり、$T(q) = p_wq$とされます。また、2部料金(or franchise fee)とは、固定料金$A$と購入数量によって変動する部分に分けられ、$T(q)=A+p_wq$と表されます。
2.2 垂直的取引制限(Vertical Restraints)
前述の通り、小売の下す意思決定が直接的に製造業者の利潤に影響するため、製造業者は下流企業である小売を何らかの形でコントロールするインセンティブを持ちます。ここでは、垂直的取引制限の4つの種類を簡単に紹介します。
1. 再販売価格維持(Resale-Price maintenance; RPM)
RPMは、下流企業が消費者へ販売する価格$p$を上流企業が決定し、強制するものです。この場合、上流企業にとって最適な最終財価格$p$を決めることができますが、下流企業にとっては利潤がほとんどなくなってしまうため、一部の産業(新聞配達など)を除いて法律で禁止されています。
また、RPMのバリエーションとして、価格の底(floor)を定めるもの、価格の天井(ceiling)を定めるものがあります。
2. 販売数量固定(Quantity fixing)
販売数量固定では、下流企業が上流企業から購入する中間財の量$q$を指定・固定します。上流企業にとって、価格を指定するのか、販売数量を指定するのかは本質的に同じものになるため、今後の分析ではRPMのみに焦点を当てます。また、RPM同様、数量の底を定めるもの、数量の天井を定めるものがバリエーションとしてあります。
3. テリトリー制(Exclusive territories)
下流企業が複数ある場合、下流企業どうしで価格競争(数量競争でも同じです)が発生することで、下流企業にとっての最終的な利潤は減少し、これは上流企業の利潤低下にも間接的につながります。この場合、上流企業が複数の下流企業の間で市場を分割し、それぞれの下流企業がそれぞれの市場で独占となる状態を作り出すことで、上流企業は自らの利潤を増加させることができます。これは、例えば下流企業を北海道と沖縄にするなど、物理的に遠い場所にすることで実現されています。
4. 専売店制(Exclusive dealing)
下流企業どうしの競争を緩和させるための2つ目の手段として、専売店制があります。これは、1つの下流企業に対して1つのブランドの製品のみを卸すことで、ブランド間での競争(Interbrand Competition)を緩和させる目的があります。
3. 外部性 (Externalities) と垂直的コントロール (Vertical Control)
ここでは、上流企業と下流企業の利潤の合計をaggregate profitと呼び、aggregate profitに直接影響を与える要因に焦点を当てて分析します(例えば、$p_w$は間接的には影響を与えますが、直接的には影響を与えないため、分析のtargetとはしません)。
そして、重要な仮定として、下流企業にとっての“outside opportunity”は0とします。これは、下流企業が上流企業からの契約の提案を、もしそれを受け取った場合に利潤が負にならない場合にのみ、提案を受け取るということです。つまり、上流企業の提案以外に、全く別のビジネスプランがあり、そちらを優先する、といったことがないと仮定しています。
3.1 例 1:二重マージンの問題 (Spengler 1950)
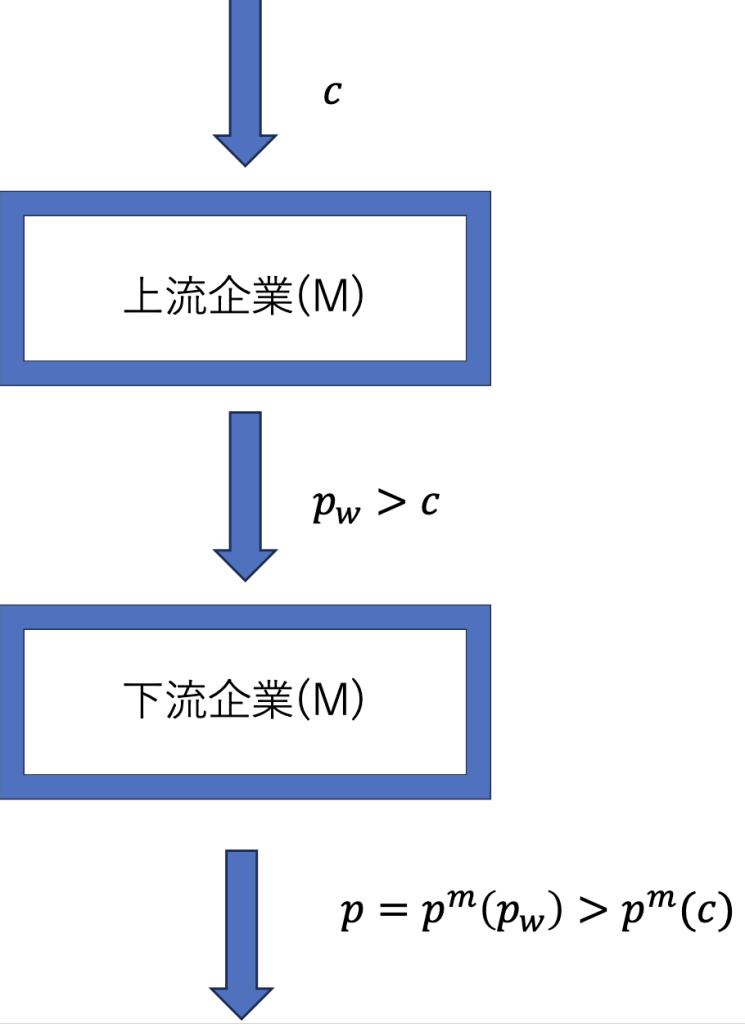
ここでは、上流企業と下流企業がそれぞれ 1 社の場合を考えます。この場合、両企業はそれぞれの市場に対して独占であり、市場支配力を持っています。以下の図が、現在考えている垂直的市場の構造を視覚化したものです。
図 1 二重マージン
ここで、(M)は、Monopolistであることを意味しています。また、上流企業は中間財に対して、線形価格$T(q)=p_wq$を課すとしています。上流企業は下流企業に対して独占なので、限界費用よりも高い価格をつけます($p_w>c$)。下流企業にとっての限界費用は、卸売価格(中間財価格)である$p_w$になります。下流企業が中間財への需要を増やした時に、それによって上流企業の利潤は$p_w-c$だけ増えますが、このことを垂直的な外部性(vertical externality)と言います。しかし、下流企業は自らの利潤を最大にすることのみを考えており、自分の行動が上流企業の利潤へ与える影響を考慮していないために、社会的に望ましい中間財の需要量よりも過小に需要してしまいます。この問題は、下流企業にとっての限界費用$p_w$が上流企業の限界費用$p_w$と異なるために発生してしまいます。
この垂直的な外部性による問題を考えるために、まず、垂直統合された場合の生産量と価格を以下のように定義します。
\begin{equation}
q^m = D(p^m)……(1)
\end{equation}
ここで、$p^m$は$(p-c)D(p)$を最大化するような価格で、$D(\cdot)$は需要曲線です。
次に、垂直的に分離されている市場構造での生産量と価格を考えます。下流企業にとっての限界費用は$p_w$であることから、下流企業は以下の最大化問題を解くことになります。
\begin{equation}
\text{max}_{p}\quad (p-p_w)D(p)……(2)
\end{equation}
つまり、利潤を最大化するように価格$p$を選びます。ここで、下流企業は消費者に対して独占であるため、利潤最大化の結果選ばれる価格は限界費用よりも高いため、$p>p_w$となります。上流企業も同様に、下流企業に対して独占であるために、
\begin{equation}
\text{max}_{p_w}\quad (p_w-c)D(p)……(3)
\end{equation}
の結果は、$p_w>c$となります。以上の結果を合わせると、$p>p_w>c$となることがわかります。
ここで、下流企業が価格$p$を下げた時は需要が増加することに注意すると、($dp<0$とすると)$D'(p)>0$になります。よって、下流企業が価格を下げた場合、上流企業の利潤は$(p_w-c)D'(p)>0$だけ増加しますが、下流企業はこのことを考慮しないで意思決定を行うために(社会的には)過小な生産量になってしまうことが推測できます。以下では、需要関数を$D(p)=1-p$と特定化して以上の結果を確かめてみます。
下流企業は、
\begin{equation}
\text{max}_{p}\quad (p-p_w)(1-p)……(4)
\end{equation}
を解きます。最大化の一階条件より、
\begin{equation}
p=\frac{1+p_w}{2}……(5)
\end{equation}
を得ることができます。下流企業は消費者の需要量だけ中間財を購入するので、中間財の購入量は
\begin{equation}
q = 1 – p = \frac{1-p_w}{2}……(6)
\end{equation}
となります。これより、下流企業の利潤は以下の通りです。
\begin{equation}
\Pi_m = (p-p_w)q = \left(\frac{1-p_w}{2}\right)^2……(7)
\end{equation}
次に、ここまでの結果を所与に、上流企業の利潤最大化問題を考えます。
\begin{equation}
\text{max}_{p_w}\quad (p_w-c)\frac{1-p_w}{2}……(8)
\end{equation}
一階条件より、
\begin{equation}
p_w = \frac{1+c}{2}……(9)
\end{equation}
が得られます。よって、上流企業の利潤と最終財の価格は以下の通りになります。
\begin{equation}
\Pi_m = (\frac{1+c}{2}-c)\frac{1-\frac{1+c}{2}}{2} = \frac{(1-c)^2}{8}……(10)
\end{equation}
\begin{equation}
p = \frac{3+c}{4}……(11)
\end{equation}
上流企業と下流企業の利潤の合計を$\Pi^{ni}$とすると、
\begin{equation}
\Pi^{ni} = \Pi_m+\Pi_m = \frac{(1-c)^2}{8}+\frac{(1-c)^2}{16} = \frac{3}{16}(1-c)^2……(12)
\end{equation}
となります。最後に、垂直統合された際の利潤(1社による独占利潤)を計算するため次の最大化問題を考えます。
\begin{equation}
\text{max}_p\quad (p-c)(1-p)……(13)
\end{equation}
最大化の一階条件より
\begin{equation}
p = \frac{1+c}{2}……(14)
\end{equation}
\begin{equation}
\Pi^i = \frac{(1-c)^2}{4} > \Pi^{ni}……(15)
\end{equation}
がわかります。よって、垂直統合された場合の合計利潤の方が高いかつ、価格も垂直統合された場合の方が低いので、消費者にとっても垂直統合の場合が望ましいことがわかります。この問題は、下流企業と上流企業がそれぞれ独占者であるため、二重のマージン(財の価格が限界費用よりも高いこと)が発生していることが原因です。
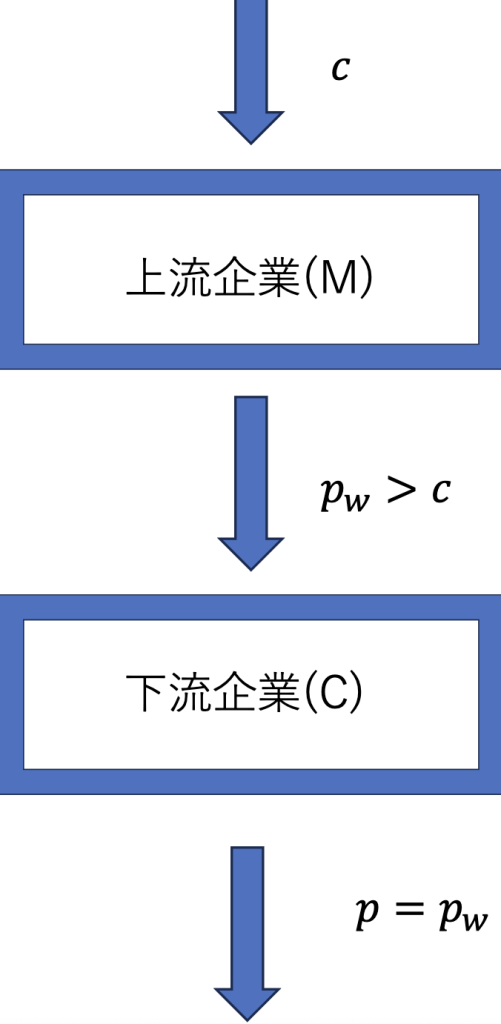
この場合だと、上流企業が下流企業に$p=p_w$を強制するようなRPMを行うことで、垂直的外部性を解決することができます。なぜなら、下流企業にとってこれは価格=限界費用を強制されるものであり、マージンを作れないことから利潤を得ることができません。これによって価格の歪みが緩和され、二重マージンの問題は解消されます。この場合の市場構造を図に表すと、以下の通りです。ここで、(C)は“Competitive”であり、競争的であることを示しています。
3.2 例 2:下流企業によるモラルハザードの問題(Downstream Moral Hazard)
次に、下流企業が、上流企業から供給される財を消費者にとってより魅力的に見えるよう努力することで需要を増加させることができる状況を分析します。これは“promotional effort”もしくは“services”と呼ばれるため、本稿では「サービス」とします。サービスの例をいくつか示します。
・ 商品の無料配達
・ スタンプカード
・ 販売前の情報公開
これらの販売促進行為によって、需要が伸びると仮定します。つまり、サービスを$s$、新しい需要関数を$q = D(p,s)$とすると、$\partial D(p,s)/\partial s>0$ということです。当然、下流企業によるサービスにはコストが伴います。サービス一単位あたりのコストを$\Phi(s)$とすると、サービスによる合計のコストは$s\Phi(s)$で表すことができます。
この垂直的市場構造において、望ましいのは垂直統合された場合の価格$p^m$、サービス$s^m$であり
\begin{equation}
(p-c-\Phi(s))D(p,s)……(16)
\end{equation}
を最大にするものとして得ることができます。よって、垂直統合された場合の利潤(vertically integrated profit)は
\begin{equation}
\Pi^m = (p^m-c-\Phi(s^m))D(p^m,s^m)……(17)
\end{equation}
となります。
次に、垂直統合されていない場合を考えます。上流企業の利潤は
\begin{equation}
(p_w-c)D(p,s)……(18)
\end{equation}
であり、下流企業の利潤は
\begin{equation}
(p-p_w-\Phi(s))D(p,s)……(19)
\end{equation}
となります。よって、下流企業によるサービスが、上流企業の利潤へ及ぼす影響は
\begin{equation}
(p_w-c)\frac{\partial D}{\partial s}>0……(20)
\end{equation}
となり、垂直的な外部性(vertical externality)が発生していることがわかります(なぜなら、下流企業はサービスが上流企業へポジティブな影響を与えることを考慮しないでサービスの量を決めるため、社会的に望ましいサービス量$s^m$よりも過小にサービスを供給することになるためです)。
この問題を解決するための方法として、RPMは十分ではありません。なぜなら、仮に上流企業が最も望ましいサービス量$s^m$を下流企業に課したとしても、実際にどの程度のサービスを行ったのかは上流企業には判断することができません。これは、下流企業によるモラルハザードの問題に相当します。そのため、上流企業にとって望ましい価格$p=p^m$を強制・監視することはできても、サービスについては下流企業の行動を正確に把握することが(通常は)困難なため、上流企業にとっての最も望ましい利潤$\Pi^m$を実現することはできません。
ここでは、2部料金(or franchise fee)を使用することで上流企業は$\Pi^m$を実現することができます。つまり、中間財の価格を$p_w=c$と設定し、下流企業が消費者に対して限界費用$c$で独占利潤を得て、最後に固定料金として$A=\Pi^m$を課すことで上流企業の利潤は$\Pi^m$となります。この場合、図2と反対の市場構造(つまり、上流企業が“C”で、下流企業が“M”ですが、最後に上流企業が固定料金として、独占利潤を全て掻っ攫う形になっています。また、この場合、片方の企業が“Competitive”になっていることから価格の歪みが解消され、垂直的な外部性も解消されていると同時に、社会厚生(Welfare)も改善されていることがわかります。
4. 最後に
本稿では、上流企業(製造業者)と下流企業(小売店)の関係を表す、Vertical structureについて簡単に見てきました。このような垂直的な関係は現実世界でも多く見られます。例えば、車の製造業者(日産、トヨタ、etc)と車のディーラーや、漁師(or 農家)とスーパー、家電製造業者と家電量販店、などです。このような垂直的な関係に直面した際、上流企業の市場支配力が強い場合、下流企業は上流企業の決定に逆らえない場合やその逆など、現実ではより複雑な関係ですが、その本質的な性質について理解して、それを応用して意思決定に役立てればと思います。
References / 参考文献
石橋孝次(2021) 産業組織ー理論と実証の接合』 慶應義塾大学出版会
Tirole, J. (1988). The theory of industrial organization. MIT press.