問題1
均衡では,$L^s = L_1+L_2$が実現します.
よって,名目賃金は,$L_1+L_2 = a\frac{a}{p}\Leftrightarrow w = \frac{p}{a}(L_1+L_2)$となります.
また,Kは一定なので定数扱いになります.
このことに注意して,企業2の利潤を考えると,企業1,2はプライステイカーなので
\begin{align*}
\pi_2 &= pq_2 – wL_2 -rK_2\\
&= pK_2L_2 -\frac{p}{a}(L_1+L_2)L_2-rK_2
\end{align*}
となります.ここで,企業2の利潤最大化の一階条件より,
\begin{align*}
\frac{\partial \pi_2}{\partial L_2} = pK_2 – \frac{p}{a}(L_1+2L_2)=0\\
\Leftrightarrow L_2 = \frac{aK_2-L_1}{2}
\end{align*}
を得ます.企業2の利潤において,$rK_2$はサンクコストであり,
操業停止条件には含まれないことに注意すると,
企業2の操業停止条件は,
$pq_2 – wL_2>0\Leftrightarrow pKL_2 -\frac{p}{a}(L_1+L_2)L_2>0$です.
これを変形していくと,
\begin{align*}
pK_2L_2 -\frac{p}{a}(L_1+L_2)L_2>0\\
K_2 > \frac{L_1+L_2}{a}\\
aK_2 – L_1 > L_2
\end{align*}
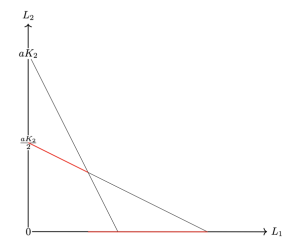
になります.横軸が$L_1$,縦軸が$L_2$のグラフに描画するため,$L_2$に関する式に変形させました.
これより,企業2が操業するための条件は,$aK_2 – L_1 \le L_2$とわかるので,
この範囲での$L_2 = \frac{aK-L_1}{2}$が企業2の労働需要量を表します.
つまり,企業2の労働需要量$L_2$は,
\begin{align*}
L_2 = \left\{
\begin{array}{ll}
\frac{aK_2-L_1}{2} & \text{if}\quad aK_2 – L_1 \le L_2
0 & \text{if}\quad aK_2 – L_1 > L_2
\end{array}
\right.
\end{align*}
になります.これをグラフに描画すると以下の通りです.
赤線の箇所が企業2の労働需要量を示します.
(2)
買手独占が労働市場で生じている場合,$L^s > L_1+L_2$になります.
(1)での企業2に関する利潤最大化問題は企業1についても同様なので,
企業1の最適反応は,$L_1 = \frac{aK_1-L_2}{2}$になります.
これと,企業2の最適反応である$L_2 = \frac{aK_2-L_1}{2}$を連立して解くと,
クールノー均衡が求められます.
よって,クールノー均衡での労働投入量($L_1^*,L_2^*$)は,
\begin{align*}
L_1 &= \frac{aK_1}{2}-\frac{aK_2}{4}+\frac{L_1}{4}\\
\frac{3}{4}L_1 &= \frac{a}{4}(2K_1-K_2)\\
\Rightarrow L_1^* &= \frac{a}{3}(2K_1-K_2)\\
L_2 &= \frac{aK_2}{2}-\frac{a}{6}(2K_1-K_2)\\
&= \frac{3aK_2-2aK_1+aK_2}{6}\\
\Rightarrow L_2^*&= \frac{a}{3}(2K_2-K_1)
\end{align*}
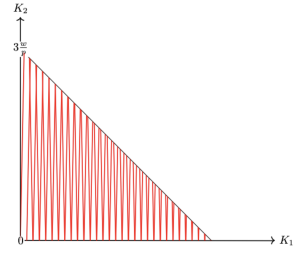
となります.これと,買手独占が労働市場で生じる条件より,
\begin{align*}
a\frac{w}{p} > L_1^*+L_2^* = \frac{a}{3}(2K_1-K_2)+\frac{a}{3}(2K_2-K_1) = \frac{a}{3}(K_1+K_2)\\
\Leftrightarrow 3\frac{w}{p} > K_1+K_2
\end{align*}
を得ます.これが,労働市場のクールノー均衡において買手独占が生じる条件を最も簡潔な不等式で表したものです.
また,条件を満たす領域は以下の通りです.