非線形関数について
関数 \(y = f(x)\) が \(x\) の1乗以外の累乗を含む項を持つ場合、それは非線形関数になります。たとえば、
\[y = x^3\]
は非線形関数であり、
\[y = 4 + x^{0.3}\]
も非線形関数です。しかし、
\[y = 7 + 0.3x\]
は線形関数です。
非線形関数はさまざまな形を取ることができますが、経済変数の関数を見る際に役立ついくつかの形状についてのみ考慮します。関数 \(y = f(x)\) が \(x\) の累乗を1より大きい何かで持つ項が1つある場合、\(x\) が正の値を取る限り、\(x\) を増加させると増加率が上昇します。
これは下記の表から明らかです。関数 \(y = x^3\) や \(y = x^4\) のグラフは上向きにカーブします。なぜなら \(y\) は \(x\) よりも速い割合で増加するからです。これらの関数はすべて原点を通ります。\(\ x\) が0のとき \(y\) も0だからです。表は \(x\) の累乗が大きくなるほど \(y\) がより速く上昇することを示しています。
経済学における非線形関数の特性
経済学では、働いている数量はしばしば正の値に制限されます。例えば、価格や数量などです。しかし、変数が負の値を取ることが許される場合、関数 \(y = x^2\) と \(y = x^3\) は、\(x < 0\) のとき、\(x^2 > 0\) だが \(x^3 < 0\) となり、異なる形状を示します。
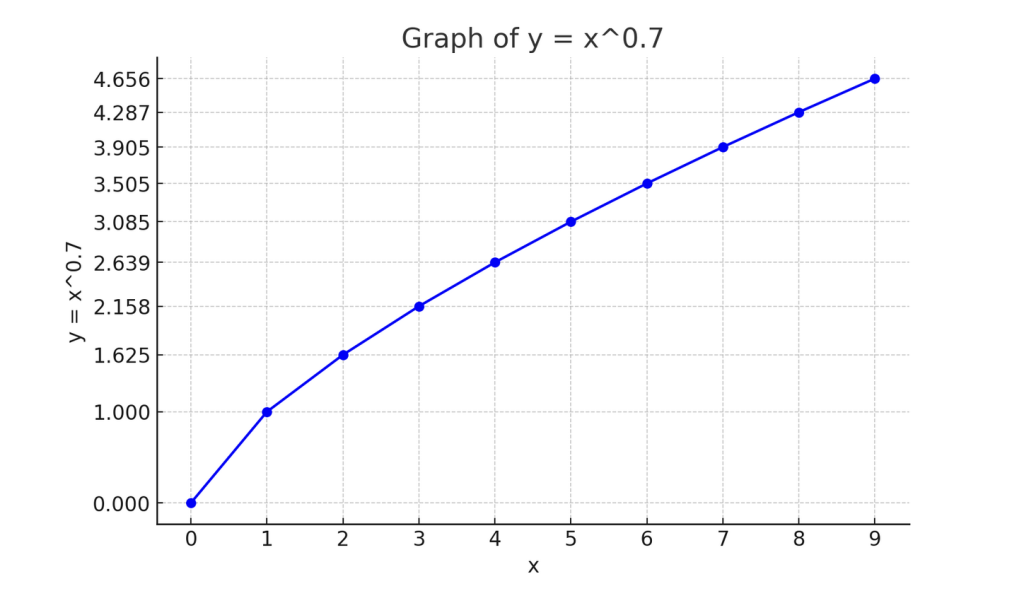
関数内の \(x\) の累乗が0と1の間にある場合、\(x\) が正である限り、関数の値は \(x\) が大きくなるにつれて増加しますが、その増加率はだんだんと小さくなります。関数 \(y = x^{0.7}\)(正のべき根のみを考慮)についての値は、この増加の遅さを示しています。
関数内の \(x\) の累乗が負の場合、\(x\) が正である限り、関数のグラフは下向きの傾斜を持ち、原点に凸の曲線の形を取ります。これらの関数の \(y\) の値は、\(x\) がゼロに近づくにつれて大きくなります。
平方根関数の例
\(x\) と \(y = x^{0.7}\) の例
| \(x\) | \(y = x^{0.7}\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1.624 |
| 3 | 2.080 |
| 4 | 2.410 |
| 5 | 2.669 |
| 6 | 2.882 |
| 7 | 3.062 |
| 8 | 3.218 |
| 9 | 3.356 |
負の累乗関数の例
\(x\) と \(y = x^{-1}\) 及び \(y = x^{-1.5}\) の例
- \( x=1 \) のとき、 \( y=1 \)
- \( x=2 \) のとき、 \( y=0.5 \)
- \( x=3 \) のとき、 \( y \approx 0.333 \)
- \( x=4 \) のとき、 \( y=0.25 \)
- \( x=5 \) のとき、 \( y=0.2 \)
- \( x=6 \) のとき、 \( y \approx 0.167 \)
- \( x=7 \) のとき、 \( y \approx 0.143 \)
- \( x=8 \) のとき、 \( y=0.125 \)
- \( x=9 \) のとき、 \( y \approx 0.111 \)
- \( x=10 \) のとき、 \( y=0.1 \)
- \( x=30 \) のとき、 \( y \approx 0.033 \)
- \( x=50 \) のとき、 \( y=0.02 \)
- \( x=70 \) のとき、 \( y \approx 0.014 \)
- \( x=100 \) のとき、 \( y=0.01 \)
関数 \( y = x^{-1.5} \) の場合
- \( x=1 \) のとき、 \( y=1 \)
- \( x=2 \) のとき、 \( y \approx 0.354 \)
- \( x=3 \) のとき、 \( y \approx 0.192 \)
- \( x=4 \) のとき、 \( y=0.125 \)
- \( x=5 \) のとき、 \( y \approx 0.089 \)
- \( x=6 \) のとき、 \( y \approx 0.068 \)
- \( x=7 \) のとき、 \( y \approx 0.054 \)
- \( x=8 \) のとき、 \( y \approx 0.044 \)
- \( x=9 \) のとき、 \( y \approx 0.037 \)
- \( x=10 \) のとき、 \( y \approx 0.032 \)
- \( x=30 \) のとき、 \( y \approx 0.0061 \)
- \( x=50 \) のとき、 \( y \approx 0.0028 \)
- \( x=70 \) のとき、 \( y \approx 0.0017 \)
- \( x=100 \) のとき、 \( y=0.001 \)
これらの値は、 \( x \) が増加するにつれて、 \( y \) が減少することを示しています。特に、 \( x \) が大きくなるにつれて、 \( y=x^{-1.5} \) の減少速度はより急であることがわかります。