問題
総需要 \(Y_d\) は \(Y_d = C + I + G\) で表されます。
投資 \(I\) は 300、政府支出 \(G\) は 400 です。
消費 \(C\) は可処分所得に依存し、\(C = 100 + 0.75(Y – T)\) で表されます。
税金 \(T\) は所得 \(Y\) に依存し、\(T = 0.2Y\) で与えられます。
均衡国民所得を求めるには、総需要 \(Y_d\) が総供給 \(Y_s\) と等しいときの国民所得 \(Y\) を求めます。この場合、総供給 \(Y_s\) は国民所得 \(Y\) そのものと考えることができます。つまり、\(Y_d = Y_s = Y\) です。
まず、税金 \(T\) の式 \(T = 0.2Y\) を消費 \(C\) の式に代入します。
\(C = 100 + 0.75(Y – T) = 100 + 0.75(Y – 0.2Y)\)
次に、総需要の式 \(Y_d = C + I + G\) にこれらの値を代入します。
\(Y = 100 + 0.75(Y – 0.2Y) + 300 + 400\)
この方程式を解いて \(Y\)、つまり均衡国民所得を求めます。
均衡国民所得 \(Y\) は 2000 です。
これは、総需要と総供給が等しいとき、国民所得が 2000 の水準で均衡することを意味します。この計算により、市場が均衡状態に達する点での国民所得の水準を求めることができました。
均衡国民所得を求めるための計算ステップ
ステップ 1: 消費 \(C\) の式に税金 \(T\) を代入する
まず、税金 \(T = 0.2Y\) の式を消費 \(C\) の式に代入します。消費は \(C = 100 + 0.75(Y – T)\) で表され、ここで \(T = 0.2Y\) です。これを代入すると、
\[C = 100 + 0.75(Y – 0.2Y)\]
となります。これをさらに単純化すると、
\[C = 100 + 0.75(0.8Y)\]
\[C = 100 + 0.6Y\]
となります。
ステップ 2: 総需要 \(Y_d\) の式に値を代入する
総需要は \(Y_d = C + I + G\) です。ここで \(C\)、\(I\)、\(G\) の値を代入します。\(I = 300\)、\(G = 400\) です。そして、ステップ 1 で計算した \(C\) の値も代入します。
\[Y_d = (100 + 0.6Y) + 300 + 400\]
これをさらに単純化します。
\[Y_d = 800 + 0.6Y\]
ステップ 3: 総需要 \(Y_d\) と総供給 \(Y_s\) が等しいときの \(Y\) を求める
総供給 \(Y_s\) は国民所得 \(Y\) そのものです。つまり、\(Y_d = Y\) の時に均衡が成立します。よって、次の方程式を解きます。
\[Y = 800 + 0.6Y\]
ステップ 4: 方程式を解く
この方程式を整理すると、
\[0.4Y = 800\]
両辺を 0.4 で割ることで、\(Y\) を求めます。
\[Y = 2000\]
以上の計算により、均衡国民所得は 2000 であることが分かります。これは、総需要と総供給が等しくなる点での国民所得の水準を示しています。
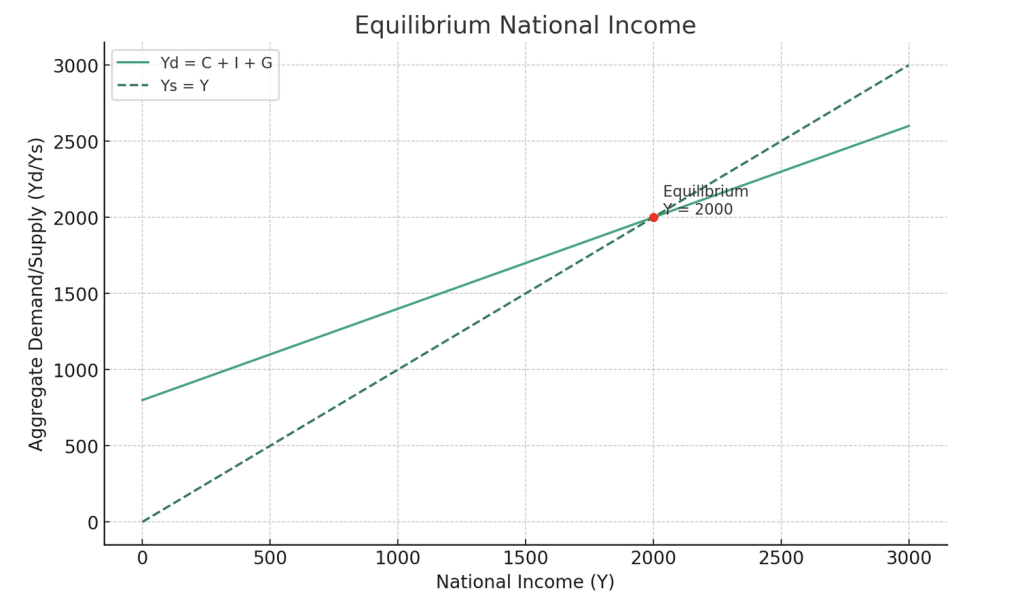
上記の図は、国民所得(Y)をx軸に、総需要(Yd)と総供給(Ys)をy軸にして、均衡国民所得の概念を視覚化しています。総需要の曲線は「Yd = C + I + G」の式に基づいて描かれ、総供給の曲線は45度の直線「Ys = Y」として表されています。これら二つの曲線が交差する点が均衡点であり、この点での国民所得(Y)は2000であることを示しています。