二項分布は、独立な試行を複数回行い、各試行である事象(例えばコインの表が出ること)が起こるか否かを調べる際に使用される確率分布です。試行回数 \(n\) が増えると、二項分布はある条件の下で正規分布に近似されるようになります。この近似は、中心極限定理の一例です。具体的には、試行回数 \(n\) が大きく、成功確率 \(p\) が \(0\) にも \(1\) にも非常に近くない場合(一般的には \(np\) と \(n(1-p)\) がどちらも \(5\) 以上である場合)に、二項分布は正規分布に近似できます。
具体例
例えば、コインを投げる場合を考えましょう。このコインが表になる確率を \(p = 0.5\) とします。コインを \(10\) 回投げる場合(\(n = 10\))と、\(100\) 回投げる場合(\(n = 100\))について、二項分布と正規分布の近似を比較してみましょう。
– \(n = 10\) の場合:
– この場合、表が出る回数 \(X\) の確率分布は二項分布 \(B(10, 0.5)\) に従います。しかし、\(n = 10\) ではまだ正規分布に近似するには少し小さいため、確率分布の形状は正規分布ほど滑らかではありません。
– \(n = 100\) の場合:
– ここでは表が出る回数 \(X\) の確率分布は二項分布 \(B(100, 0.5)\) に従います。この場合、\(np = 50\) および \(n(1-p) = 50\) となり、二項分布は正規分布に近似される条件を満たします。したがって、\(X\) の分布は平均 \(50\)、標準偏差 \(\sqrt{100 \times 0.5 \times (1-0.5)} = 5\) の正規分布に近似できます。
それでは、これらの条件の下での二項分布のグラフと、それに対応する正規分布の近似を示したグラフを描いてみましょう。まず、\(n = 10\) と \(n = 100\) の場合の二項分布を描き、その後にそれぞれについて正規分布の近似を示します。
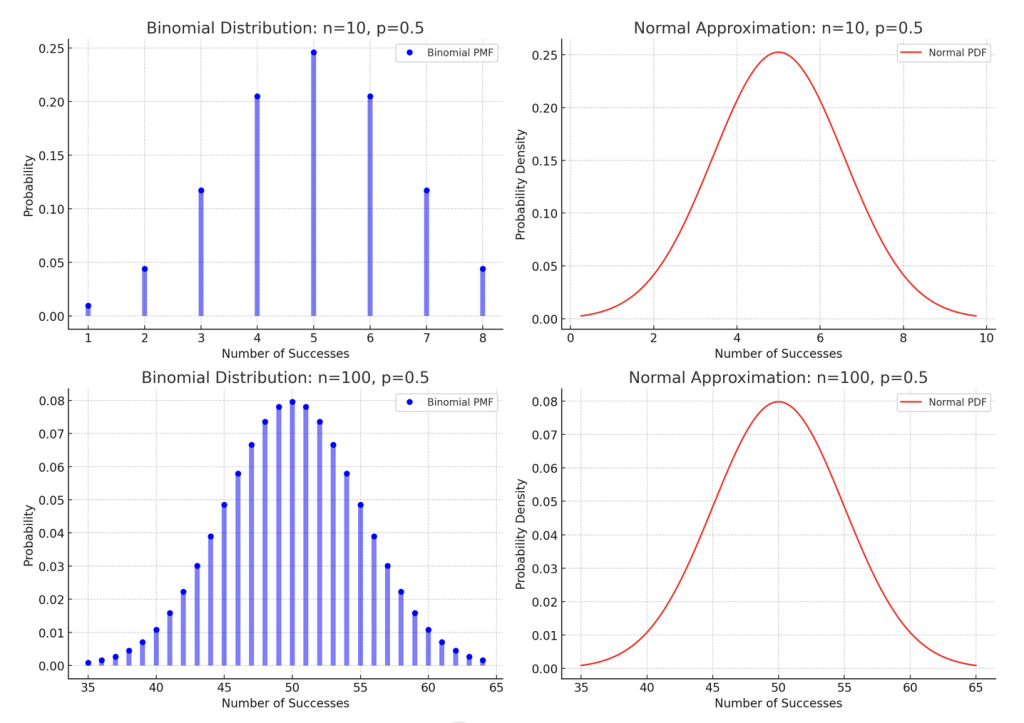
上のグラフでは、二項分布とその正規分布による近似を \(n = 10\) と \(n = 100\) の場合について示しています。各図の左側は二項分布の確率質量関数(PMF)を、右側は正規分布の確率密度関数(PDF)を表しています。
– \(n = 10\) の場合: 二項分布は正規分布ほど滑らかではありませんが、分布の形状が確率的な変動を示していることがわかります。
– \(n = 100\) の場合: このときの二項分布は正規分布にかなり近い形状をしています。特に、\(n\) が大きくなると、二項分布の形は正規分布のベル形状に近づき、その近似はより正確になります。
この例から、試行回数 \(n\) が大きくなるにつれて、二項分布は正規分布によってより良く近似できることがわかります。この性質は、大数の法則や中心極限定理と関連しており、多くの確率変数の和が正規分布に従う傾向にあることを示しています。これは、実際のデータ分析や統計的推定において重要な役割を果たします。