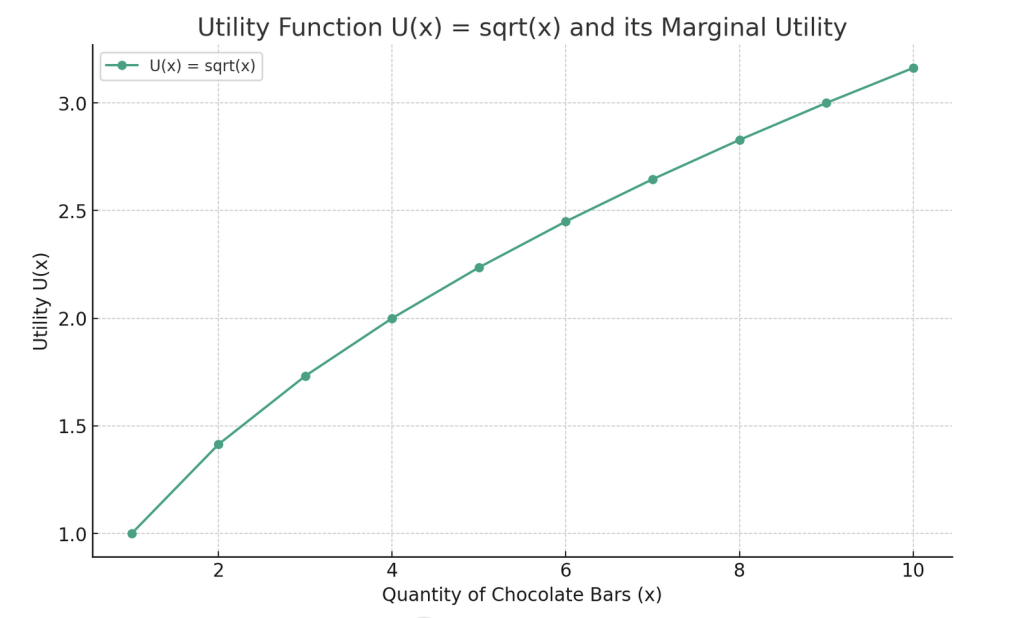
効用関数と限界効用
個々の人にとって重要なのは、経済活動の結果として得られる満足度です。この満足度を効用(U)と呼びましょう。効用は数値で測ることができ、その数値を加算したり減算したりすることが可能です。このように扱える効用を基数的効用と言います。消費量を \( x \) とすると、消費する財の効用 \( U \) は次のような関数形で表せます:
\[ U = U(x) \]
これは、効用 \( U \) が消費量 \( x \) の関数であることを意味しています。財の消費量が増えると効用も増加します。したがって、微分を用いて表現すると、
\[ \frac{dU}{dx} > 0 \]
となります。ここで \( d \) は微少量の変化を示し、\( x \) が微小単位で増加すると \( U \) も増加するため、この式の符号はプラスになります。
例:チョコレートバーの消費
限界効用の概念を説明するために、チョコレートバーの消費を例にとってみましょう。
効用関数の設定
・消費量 \( x \) を食べたチョコレートバーの数とします。
・効用 \( U \) はチョコレートバーを食べることによる満足度とします。
仮に効用関数 \( U(x) \) を \( U(x) = \sqrt{x} \) と設定しましょう。これは、チョコレートバーを食べることによる満足度が増加するものの、その増加率は消費量が増えるにつれて徐々に低下することを示しています。つまり、最初のバーは非常に高い満足度をもたらすが、その後のバーはそれほどではない。
効用の微分(限界効用)
この効用関数を \( x \) に関して微分すると、
\[ \frac{dU}{dx} = \frac{1}{2\sqrt{x}} \]
となります。この式は、チョコレートバーを1本追加するごとに得られる満足度の増加量を示しています。\( x \) の値が大きくなるにつれて、この増加量 \( \frac{dU}{dx} \) は小さくなります。つまり、最初の1本は非常に大きな満足を与えますが、5本目や6本目ではほとんど満足度が増加しないことを示しています。
限界効用の二次微分
(詳細な式展開は【限界効用の二次微分の導入】で確認できます)
限界効用の二次微分を行うと、
\[ \frac{d^2U}{dx^2} = -\frac{1}{4x^{3/2}} \]
となり、これは \( x \) が増加するにつれて限界効用がさらに減少することを示しています。
この具体例では、食べるチョコレートバーの数が増えるにつれて、追加のチョコレートバーから得られる満足度の増加がどのように減少していくかを数学的に示しています。これは「限界効用の逓減」という経済学の重要な原理であり、消費者が追加の商品やサービスを消費する際の意思決定に影響を与えます。
効用と限界効用の計算
チョコレートバーの消費に関する効用関数 \( U(x) = \sqrt{x} \) を使用して、消費量 \( x \) が1本から10本まで増加したときの効用 \( U \) と限界効用 \( \frac{dU}{dx} \) を具体的に計算してみます。
- 効用 \( U(x) \): 消費量 \( x \) に対する満足度を示します。
- 限界効用 \( \frac{dU}{dx} \): 消費量が1単位増えたときの効用の増加量です。
以下では、消費量 \( x \) が1から10までの値について、効用と限界効用を計算します。
具体的な計算は次のように行います。
- \( U(x) = \sqrt{x} \) を使用して、\( x = 1, 2, 3, \ldots, 10 \) について効用 \( U \) を計算します。
- \( \frac{dU}{dx} = \frac{1}{2\sqrt{x}} \) を使用して、同じ \( x \) 値で限界効用を計算します。
以下に、消費量 \( x \) が1本から10本までのときの効用 \( U(x) \) と限界効用 \( \frac{dU}{dx} \) の計算結果を示します。
| 消費量 \( x \) | 効用 \( U(x) = \sqrt{x} \) | 限界効用 \( \frac{dU}{dx} = \frac{1}{2\sqrt{x}} \) |
|---|---|---|
| 1 | 1.00 | 0.50 |
| 2 | 1.41 | 0.35 |
| 3 | 1.73 | 0.29 |
| 4 | 2.00 | 0.25 |
| 5 | 2.24 | 0.22 |
| 6 | 2.45 | 0.20 |
| 7 | 2.65 | 0.19 |
| 8 | 2.83 | 0.18 |
| 9 | 3.00 | 0.17 |
| 10 | 3.16 | 0.16 |
この表から、以下のことが観察できます。
・効用 \( U(x) \) は消費量 \( x \) が増加するにつれて増加しますが、増加率は次第に低下しています。
・限界効用 \( \frac{dU}{dx} \) も消費量が増加するにつれて減少しており、これは限界効用の逓減の原則を示しています。つまり、最初のチョコレートバーは高い満足度を提供しますが、その後のバーでは提供される満足度が徐々に減少します。(図1も参照)
この例を通じて、消費者が追加の商品やサービスを消費する際の意思決定がどのように影響を受けるかを理解できます。特に満足度の増加が少なくなるため、消費者はさらなる消費に対して躊躇するかもしれません。
図1