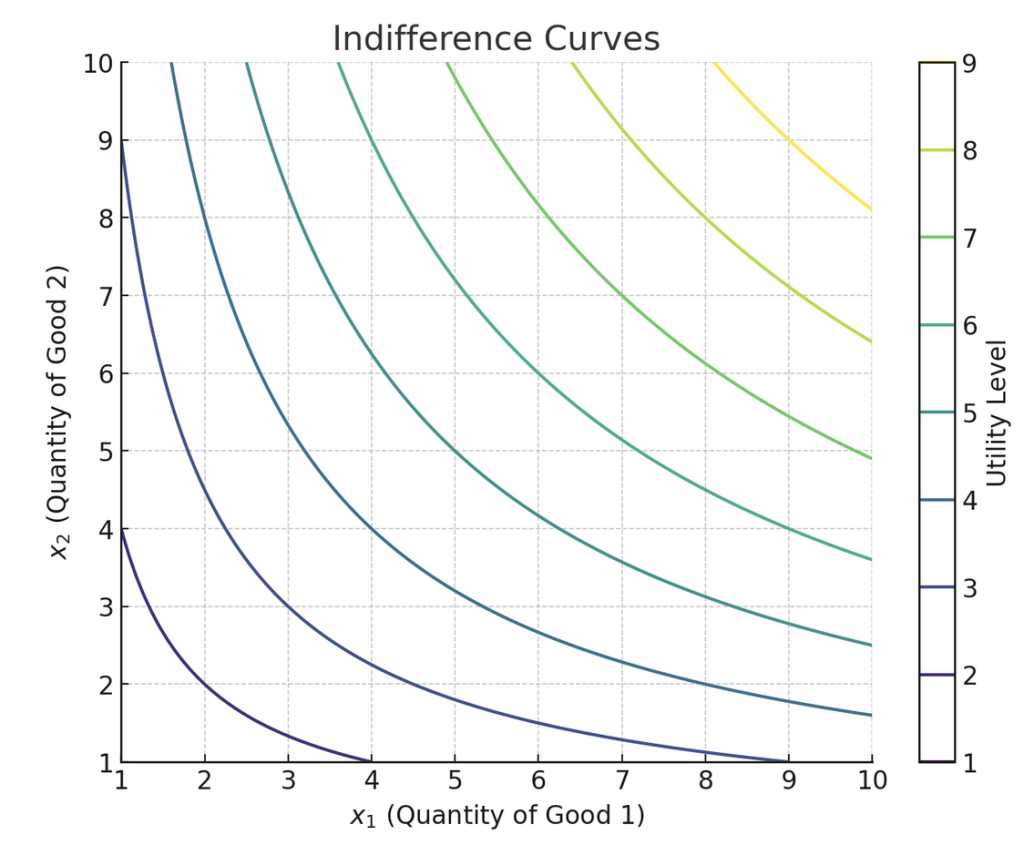
無差別曲線について説明します。
ここでは、2つの財(商品)を消費する消費者の効用関数を次のように定義します。
\[ U = U(x_1, x_2) \]
ここで、\(x_1\) は第1財の消費量、\(x_2\) は第2財の消費量を表し、\(U\) は効用水準を示します。この効用水準は、数値で具体的に表すことはできませんが、大小関係は比較可能です。
また、第1財の消費量が増えると効用は増加し、第2財の消費量が増えても同様に効用は増加します。ただし、消費量が増加するにつれて効用の増加幅は小さくなるとします。これは、追加の消費がもたらす満足度が減少するという意味です。
\( (x_1, x_2) \) 平面上の任意の点は、特定の効用水準に対応します。この平面上で、同一の効用水準を持つ点の集合を無差別曲線と呼びます。無差別曲線上のどの点を選んでも、消費者の効用水準は変わりません。つまり、無差別曲線は消費者の好みや選択の違いを示すものではなく、あくまで同じ満足度を示す異なる商品組み合わせを表す曲線です。
下記は分かりやすく色付きで書かれています。
同じ色の線がそれぞれの無差別曲線になります。
右上の線になればなるほど効用が高くなります。
また数式 \( U = U(x_1, x_2) \) の読み方は
「U イコール U カッコ エックス・ワン、エックス・ツー カッコトジ」と読みます。ここで、
– \( U \) は「効用」を表す関数です。
具体的な数値を使って、効用関数 \( U = U(x_1, x_2) \) の例を見てみましょう。
仮定として、効用関数が以下の形を持つとします。
\[ U(x_1, x_2) = x_1^{\frac{1}{2}} \times x_2^{\frac{1}{2}} \] この関数は、第1財と第2財の消費量が効用に与える影響がそれぞれ半分ずつとなるような形を示しています。この形は「コブダグラス効用関数」として知られており、一般的な例として使われます。
例えば、消費者が第1財を4単位、第2財を16単位消費する場合、効用 \( U \) を計算すると以下のようになります。
\[ U(4, 16) = 4^{\frac{1}{2}} \times 16^{\frac{1}{2}} = 2 \times 4 = 8 \]
この場合、効用水準は8となります。
一方、もし第1財を9単位、第2財を9単位消費する場合は、
\[ U(9, 9) = 9^{\frac{1}{2}} \times 9^{\frac{1}{2}} = 3 \times 3 = 9 \]
効用水準は9となり、前の例よりも高い効用を達成しています。
このように、\( x_1 \) と \( x_2 \) の値を変化させることで得られる効用水準 \( U \) を具体的に計算でき、消費者がどのような財の組み合わせを選ぶべきかを判断するための基準を提供します。また、無差別曲線はこれら同じ効用水準を得る異なる \( x_1 \) と \( x_2 \) の組み合わせを結んだ曲線として表現されます。