無差別曲線2

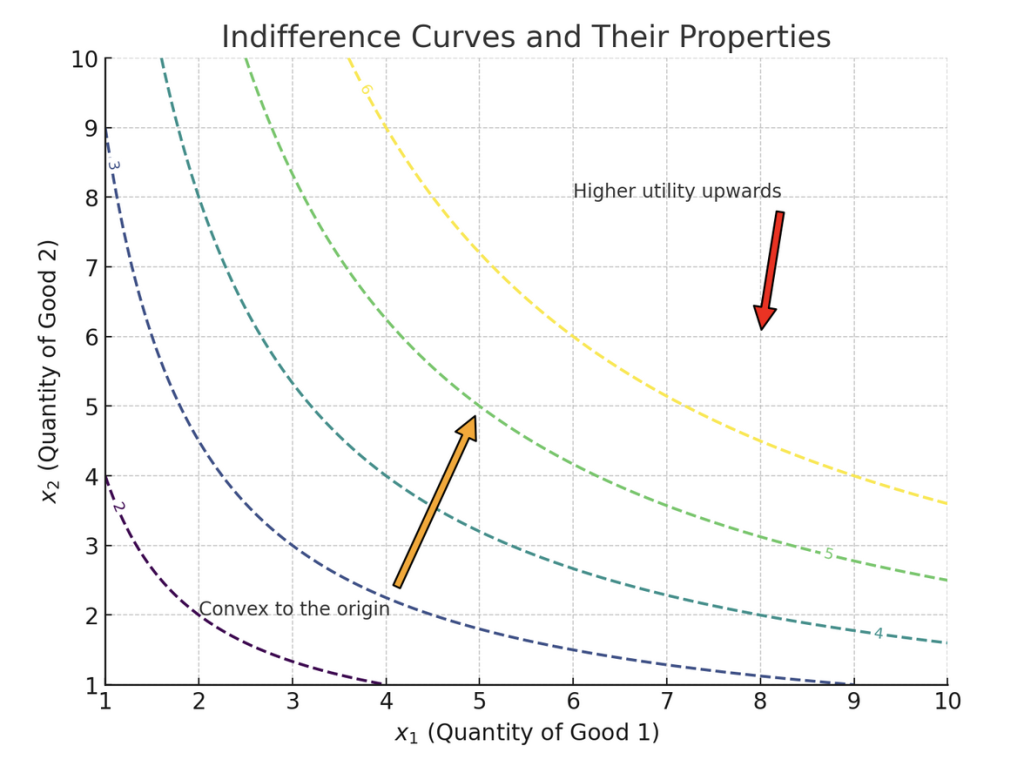
無差別曲線を考慮する際、消費者が2種類の財を消費するシナリオから出発します。

ここでの効用関数 \( U = U(x_1, x_2) \) によると、財の消費量が増加することは効用を高めるため、曲線がグラフの上部に位置するほど高い効用水準に対応します。逆に、ある財の消費量が減少すると効用も減少しますが、他の財の消費を増やすことで同じ効用を維持できるため、無差別曲線は右下がりの傾向を示します。

グラフ上のすべての点は何らかの効用水準に対応しており、無差別曲線は無数に存在することができます。理論的には、同じ点が2つの異なる効用水準に対応することはなく、したがって無差別曲線は交わることがありません。

さらに、消費量が増えるにつれて追加的な効用の増加幅は小さくなります（限界効用の逓減）。このため、同じ効用水準を達成するためには、財の代替の比率も変化する必要があります。たとえば、第1財の消費量が多い場合、第2財の消費量が少なくなるにつれて、その減少による効用の低下を補うために必要な第1財の追加消費量はより多くなります。この現象は無差別曲線の傾きが消費量に応じて変化し、曲線が原点に対して凸の形状を示す原因となります。

無差別曲線の特性を要約すると、以下の5つの特徴があります。
1. 右下がり
2. グラフの右上に位置するほど高い効用に対応
3. 曲線は互いに交わらない
4. 平面上には数多く存在する
5. 原点に対して凸の形をしている

この説明は無差別曲線の基本的な概念とその性質を理解するのに役立つでしょう。

図でも見てみましょう。