効用関数と無差別曲線

例：
– 効用が10の無差別曲線上では、リンゴ2個とオレンジ3個のバンドル $ x_1 $ と、リンゴ3個とオレンジ2個のバンドル $ x_3 $ が含まれるかもしれません。ここで、 $ u(x_1) = u(x_3) = 10 $ です。
– この無差別曲線上のどのバンドルを選んでも、消費者は同じ効用水準（同じ満足度）を得ることになります。

結局のところ、効用関数と無差別曲線は消費者の選好を説明するために用いられ、選好関係を数学的に可視化するツールとして機能します。効用関数は各商品バンドルに数値を割り当て、無差別曲線は同じ効用水準を持つバンドルを結ぶことで、消費者の選択肢をグラフ上で表現することができるのです。

無差別曲線のグラフ的表現

無差別曲線は通常、2次元グラフ上で表現されます。横軸にある商品（例えばリンゴの数）、縦軸に別の商品（例えばオレンジの数）をとり、消費者が同じ効用を得る異なる商品バンドルの組み合わせを結んだ曲線が無差別曲線です。

効用水準が異なると、曲線の位置も変わります。通常、効用が高くなるほど、無差別曲線は右上方へ移動します。これは、より多くの商品を消費することで、通常はより高い効用を得られることを示しています。

この概念は、消費者が異なる商品の組み合わせに対してどのように選好を持つかを理解するために非常に役立ちます。消費者の選択行動や、商品間のトレードオフを分析する際に重要なツールとなります。

無差別曲線の性質

1. 無数に存在する

消費者が異なる商品バンドルに対して持つ選好は、無数の無差別曲線で表現できます。これは、異なる効用水準を持つ各商品バンドルが、異なる無差別曲線上に位置することを意味します。

例：

考えられるある商品バンドルが、リンゴ2個とオレンジ3個（バンドルA）です。このバンドルに対応する効用が10だとしましょう。この場合、バンドルAは効用10の無差別曲線上に位置します。

もし、リンゴを1個追加してリンゴ3個とオレンジ3個（バンドルB）にした場合、この新しいバンドルは効用がもう少し高い別の無差別曲線（例えば効用11）上に位置します。

このように、財のバンドルが変わるごとに、新しい無差別曲線が描け、消費者の全ての選好はこれらの無差別曲線群によって覆われます。

2. 無差別曲線の方向原理

無差別曲線上の点は、消費者が同じ効用水準を感じる異なる商品バンドルを表します。2次元のグラフで考えると、横軸にある商品の量（例：リンゴの数）、縦軸に別の商品の量（例：オレンジの数）を表します。

無差別曲線が原点から北東方向にあるほど、それはより多くの商品を含むバンドルを表し、通常はより高い効用（満足度）に対応します。なぜなら、一般に、消費者はより多くの商品を持っている方が、少ない商品を持っているよりも幸福だと感じるからです。

例:

例1：無差別曲線Aがリンゴ2個とオレンジ2個のバンドルに対応するとします。この曲線上の任意の点は、効用水準が同じ異なるバンドルを表します。
例2：無差別曲線Bがリンゴ4個とオレンジ4個のバンドルに対応するとします。この曲線は曲線Aよりも原点から北東に位置しています。

この場合、曲線Bは曲線Aよりも原点から北東にあるため、より望ましいバンドル（つまり、より多くのリンゴとオレンジを含むバンドル）に対応しています。つまり、消費者は曲線B上の任意のバンドルを、曲線A上の任意のバンドルよりも好むと考えられます。

この性質は、消費者の選好をグラフ上で可視化する際に重要です。無差別曲線が原点から離れるほど、それはより多くの商品を含むバンドルを表し、消費者にとってより望ましい選択肢であることを示します。

3. 無差別曲線の連続性

無差別曲線の連続性は、消費者の選好が微小な商品の変化に対しても一貫していることを意味します。つまり、商品バンドルが少しずつ変化しても、無差別曲線上の点は滑らかに移動します。

4. 無差別曲線の右下がりの性質

無差別曲線が右下がりであることは、ある商品の量を増やすためには、別の商品の量を減らさなければならないという、消費者の選好におけるトレードオフを表します。つまり、一方の商品をもっと得るためには、もう一方をある程度犠牲にする必要があります。

例:

例1：ある消費者がリンゴとオレンジのバンドルに対する選好を考えます。無差別曲線Aがリンゴ3個とオレンジ2個に対応しているとします。
例2：もしリンゴの量を3個から4個に増やしたい場合、オレンジの量を2個から1個に減らさなければ、同じ無差別曲線A上に留まることはできません。つまり、4個のリンゴと1個のオレンジの組み合わせは、同じ効用水準を持つと見なされます。

ここで、もし無差別曲線が右上がりだったり、軸に平行だった場合、ある商品の量を増やしても、もう一方の商品の量を変えずに同じ効用を得ることができるということになり、これは単調性の原則に反します。単調性の原則は、一般的に「より多くの商品を持つほど、消費者はより満足する」という考え方に基づいています。

無差別曲線が右下がりであることは、消費者が商品間でトレードオフを行う必要があることを示し、これは現実の消費者の行動をより正確に反映しています。この性質は、消費者の選好と商品間の代替関係を理解する上で非常に重要です。

5. 無差別曲線が交差しない

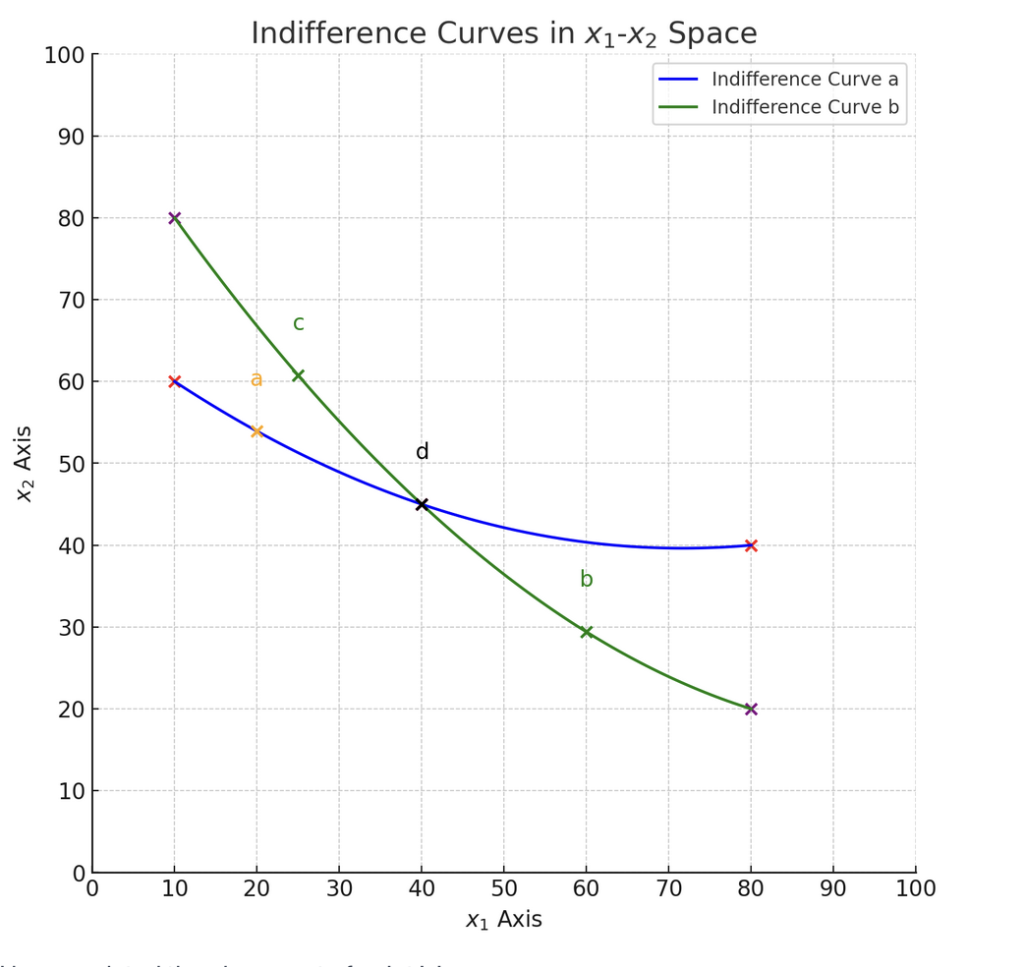
無差別曲線が交差すると、次のような矛盾が生じます：

・交差点「d」：無差別曲線AとBの交点で、二つの異なる効用水準が交わる点です。

・点「a」：無差別曲線A上の点で、ある特定の財バンドルを表します。

・点「b」と点「c」：無差別曲線B上の点で、それぞれ異なる財バンドルを表します。

もし無差別曲線が交差すると、点「a」と点「d」が同じ効用水準を持つことになります（aId）。同様に、点「b」と点「d」も同じ効用水準を持ちます（bId）。しかし、これは点「a」と点「c」が同じ効用水準を持つことを意味し、これは矛盾します（aIc）。なぜなら、点「c」は点「a」よりも少ない財を持っているため、効用水準が低いはずです（cPa）。このため、無差別曲線が交差すると、消費者の選好に矛盾が生じるため、実際には無差別曲線は交差しないとされています。

この原則は、経済学において消費者の選好が一貫性を持ち、異なる効用水準が明確に区別されることを保証します。無差別曲線が交差しないという原則は、効用と選好をモデリングする際の基本的な前提となっています。

6. 無差別曲線の凸性

$αx + (1-α)y > x $の概念

この式は、無差別曲線の凸性の原則を表現しています。ここで、$ x $ と $ y $ は異なる財バンドルを表し、$ \alpha $ は 0 と 1 の間の任意の実数です。

– $ x $：ある財バンドル（例えば、リンゴ10個とオレンジ0個）
– $ y $：別の財バンドル（例えば、リンゴ0個とオレンジ10個）
– $ \alpha $：0 から 1 までの任意の数値（例えば、0.5）

式の意味するところは、バンドル $ x $ と $ y $ の間の混合 $ \alpha x + (1-\alpha)y $ は、バンドル $ x $ よりも望ましいということです。これは、消費者が二つの極端なバンドル $ x $ と $ y $ の代わりに、その中間の何らかの組み合わせを好むことを意味します。

凸性の重要性

無差別曲線の凸性は、消費者が多様な財の組み合わせを好むという性質を示しています。例えば、消費者がリンゴだけかオレンジだけのどちらかを選ぶよりも、リンゴとオレンジの両方を含むバンドルを好むことを意味します。この凸性により、消費者の選好は多様性とバランスを重視することが示されます。

この原則は、経済学において消費者の選好が一貫性を持つことを示す重要な概念であり、効用理論において基本的な役割を果たしています。