問題3
需要関数および供給関数が以下のように与えられています。
- 供給関数: \( P = Q^2 + 5Q + 10 \)
- 需要関数: \( P = -3Q + 30 \)
均衡価格と均衡取引量を求めなさい。
解答
これらの関数を等しく設定して、均衡点を求めます。つまり、次の方程式を解く必要があります:
\[ Q^2 + 5Q + 10 = -3Q + 30 \]
この方程式を解くと、\( Q \) に対して二つの解が得られます: \( Q = -10 \) と \( Q = 2 \)。しかし、市場の文脈において、負の取引量は意味をなさないため、\( Q = -10 \) は無視します。よって、均衡取引量は \( Q = 2 \) です。
次に、この均衡取引量を供給関数に代入して均衡価格を求めます。計算すると、均衡価格 \( P \) は 24 となります。
詳細なステップ
まず供給関数と需要関数が等しい時の均衡点を求める必要があります。供給関数は \( P = Q^2 + 5Q + 10 \) 、需要関数は \( P = -3Q + 30 \) です。
均衡点を求めるには、まずこれらの関数を等しいと設定し、方程式を解きます。つまり、以下のようになります。
\[ Q^2 + 5Q + 10 = -3Q + 30 \]
これを解くために、まず方程式を整理します。両辺から -3Q を引き、10を引いて整理します:
\[ Q^2 + 8Q + 10 – 30 = 0 \] \[ Q^2 + 8Q – 20 = 0 \]
この二次方程式を解くために、二次方程式の解の公式を使用します:
\[ Q = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \]
ここで、\( a = 1 \), \( b = 8 \), そして \( c = -20 \) です。これを解の公式に代入しましょう。
二次方程式の解は解の公式を使って求められます:
\[ Q = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \]
ここで \( b^2 – 4ac \) は判別式と呼ばれ、二次方程式の解の性質を決定します。この問題では:
\[ b^2 – 4ac = 8^2 – 4 \times 1 \times (-20) = 64 + 80 = 144 \]
判別式が正なので、二つの実数解が存在します。これらの解を計算すると:
\[ Q = \frac{-8 \pm \sqrt{144}}{2 \times 1} \] \[ Q = \frac{-8 \pm 12}{2} \]
これにより、二つの解が得られます:
\[ Q = \frac{-8 + 12}{2} = 2 \] \[ Q = \frac{-8 – 12}{2} = -10 \]
二次方程式の解は \( Q = 2 \) と \( Q = -10 \) です。しかし、負の取引量は経済的に意味がないため、正の解である \( Q = 2 \) を均衡取引量として採用します。
次に、この均衡取引量 \( Q = 2 \) を供給関数または需要関数のいずれかに代入して、均衡価格 \( P \) を求めます。どちらの関数を使用しても結果は同じになるはずです。供給関数に代入してみましょう:
\[ P = 2^2 + 5 \times 2 + 10 \]
これを計算して、均衡価格 \( P \) を求めます。
均衡取引量 \( Q = 2 \) のとき、均衡価格 \( P \) は 24 です。
したがって、この市場の均衡価格は 24、均衡取引量は 2 となります。
この問題を解く際に注意すべき点は、供給関数が二次方程式であるため、解が二つ出る可能性があることです。このケースでは、一つの解が負であり、経済的に意味がないため、正の解を採用しました。また、均衡点を求める際には、供給関数と需要関数が等しいと設定し、その方程式を解く必要があります。最後に、求めた均衡取引量を供給関数または需要関数のどちらかに代入して、均衡価格を計算します。
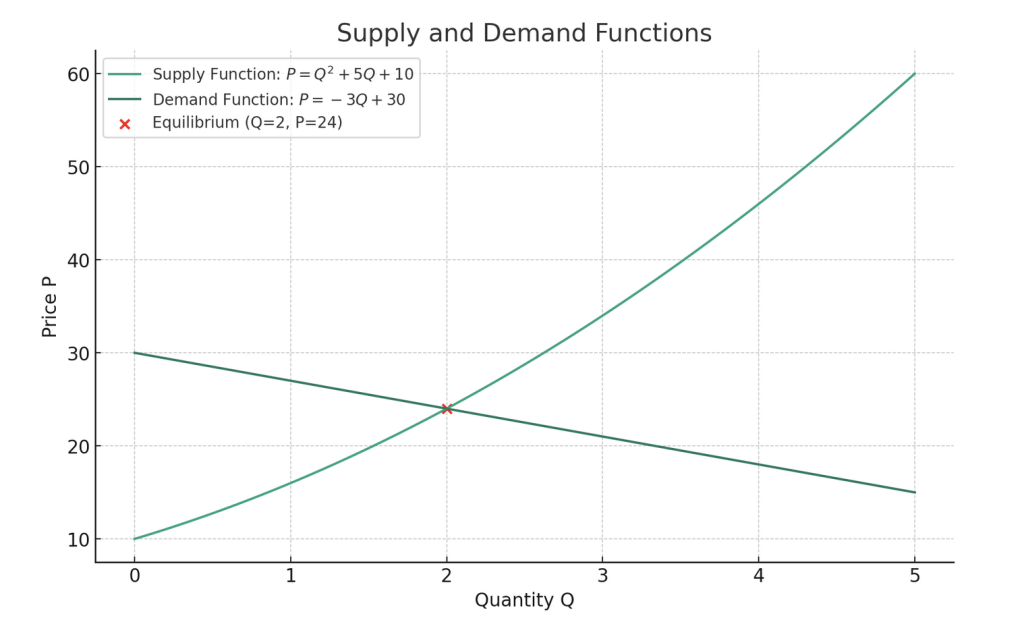
このグラフでは、供給関数(Supply Function: \(P = Q^2 + 5Q + 10\))と需要関数(Demand Function: \(P = -3Q + 30\))がプロットされています。赤い点は均衡点(Equilibrium)を示しており、ここでは取引量 \(Q = 2\)、価格 \(P = 24\) の点です。
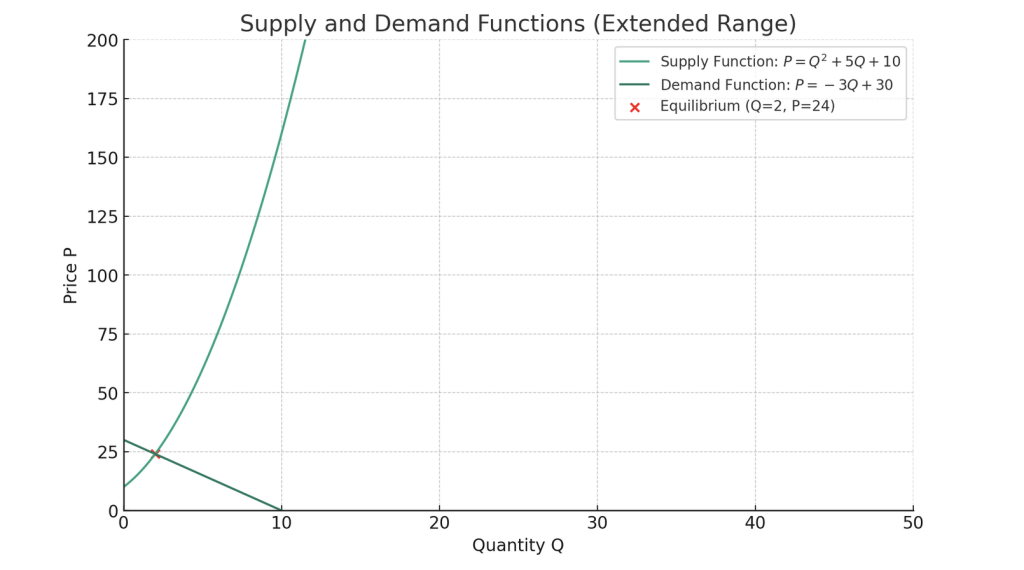
また、それぞれの関数の幅を更に取ると供給関数が直線(線形)でなく非線形( (\(Q^2\)のため)になっているのが分かります。