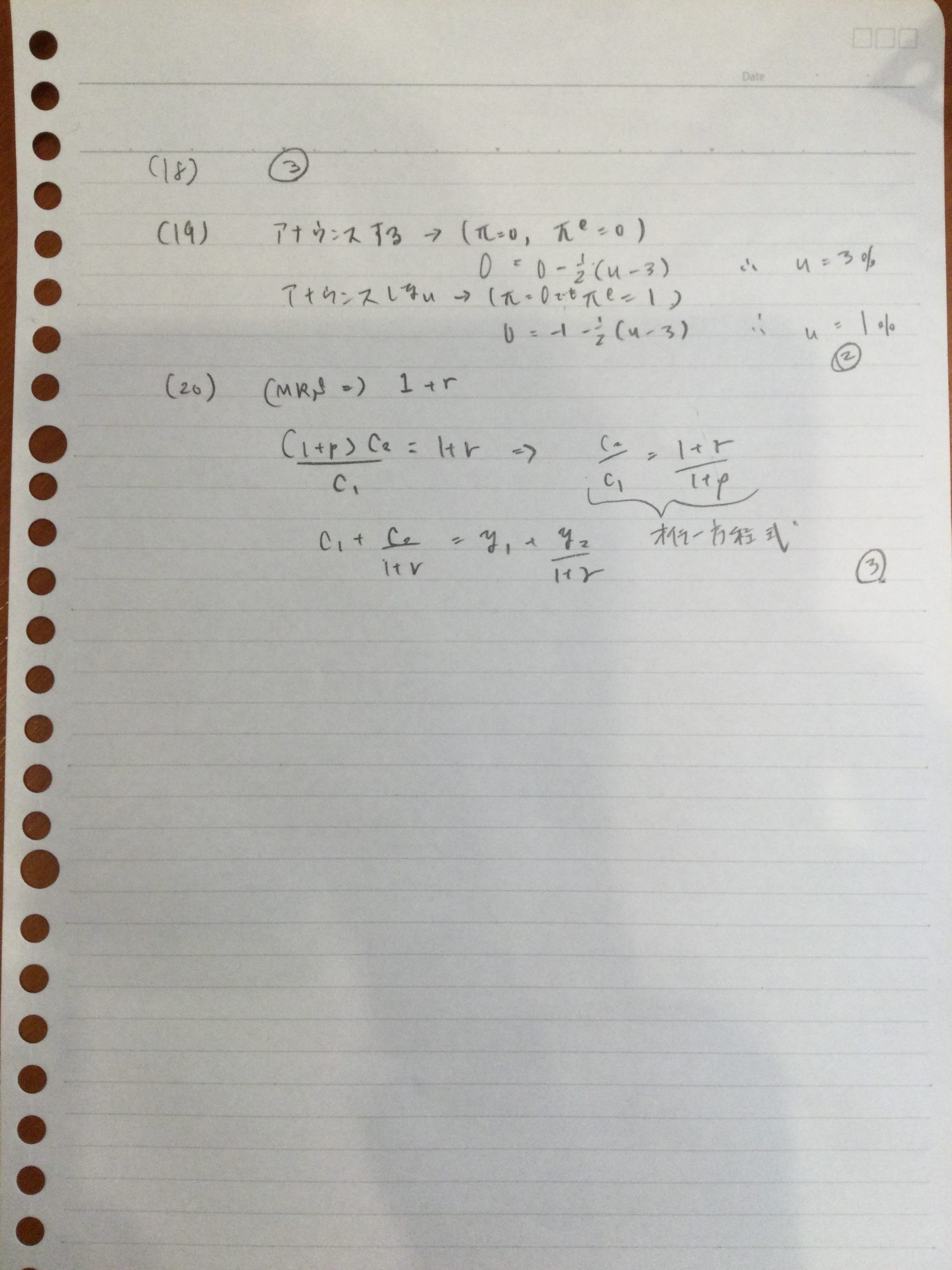*一橋大学大学院経済学研究科では2023年実施(2024年度入学)の筆記は行わず、書類・面接選考になっております。
通常の成績、研究計画書、面接対策を中心に行いましょう。
2019年度(2018年実施)
第1題
(1)
ステップ1
シェパードの補題を使う。
$$
\frac{\partial c}{\partial w_i}=\bar{x}_i(v, w, y)
$$
生産量$Y$一定の要素需要
$$
\bar{L}=\frac{\partial c}{\partial w}=\frac{2}{3} w^{-\frac{1}{3}} r^{\frac{1}{3}} Y=\frac{2}{3}\left(\frac{w}{r}\right)^{-\frac{1}{3}} Y…..【1】
$$
$$
\bar{k}=\frac{\partial c}{\partial r}=\frac{1}{3} w^{\frac{2}{3}} r^{-\frac{2}{3}} Y=\frac{1}{3}\left(\frac{w}{r}\right)^{\frac{2}{3}} Y…..【2】
$$
ステップ2
上記の式より$\frac{w}{r}$を消す。
$$
\left(\frac{w}{r}\right)^{-\frac{1}{3}}=\frac{L}{Y}{ }^{\frac{3}{2}} \Rightarrow\left(\frac{\omega}{r}\right)^{\frac{2}{3}}=\left(\frac{2 Y}{3 L}\right)^2
$$
【2】に代入して$Y$で解くと
$$
Y=3(2)^{-\frac{2}{3}} K^{\frac{1}{3}}L^{\frac{2}{3}}
$$
よって答えは①。
(2)
問題では間接効用関数が定義されています。
このとき$U$は財の価格と$m$で定義されております。
間接効用関数を$m$について解くと支出関数が得られます。
$$
m=\underbrace{3 \times 4^{-\frac{1}{3}} P_x^{\frac{2}{3}} P_y^{\frac{1}{3}} u}_{E\left(P_x, P_y, u\right)}
$$
ここでもシェパードの補題を使います。
$$
\overline{x_1}=\frac{\partial E}{\partial P_x}=2 \times 4^{\frac{1}{3}} P_x^{-\frac{1}{3}} P_y^{\frac{1}{3}} u=2 \times 4^{-\frac{1}{3}}\left(\frac{P_x}{P_y}\right)^{-\frac{1}{3}} u
$$
間接効用関数に代入、$\left(\frac{P_x}{P_y}\right)$を消す。
よって答えは①。
(3)
$$
\max _{(c, L)} u=L^{\frac{1}{2}} C^{\frac{1}{2}}
$$
$$
{ s.t. : } P C=w\left(24-L\right)+Y
$$
$$
MRS_{L C}=\frac{\frac{\partial u}{\partial L}}{\frac{\partial U}{\partial c}}=\frac{\frac{1}{2} L^{-\frac{1}{2}} C^{\frac{1}{2}}}{\frac{1}{2} L^{\frac{1}{2}} C^{\frac{1}{2}}}=\frac{C}{L}=\frac{w}{p} \Rightarrow C=\frac{w}{p} L
$$
ここで$s.t.$は$C=24 \frac{W}{P}-\frac{W}{P} L+\frac{Y}{P}$の形にでき、$C$に上記を代入。
$$
w L=w(24+L)+Y
$$
$$
2wL=24w+Y
$$
$$
L=12+\frac{Y}{2 w}
$$
$$
H =24-L=24-\left(12+\frac{r}{2 u}\right)=12-\frac{Y}{2 w}
$$
よって答えは①。
(4)
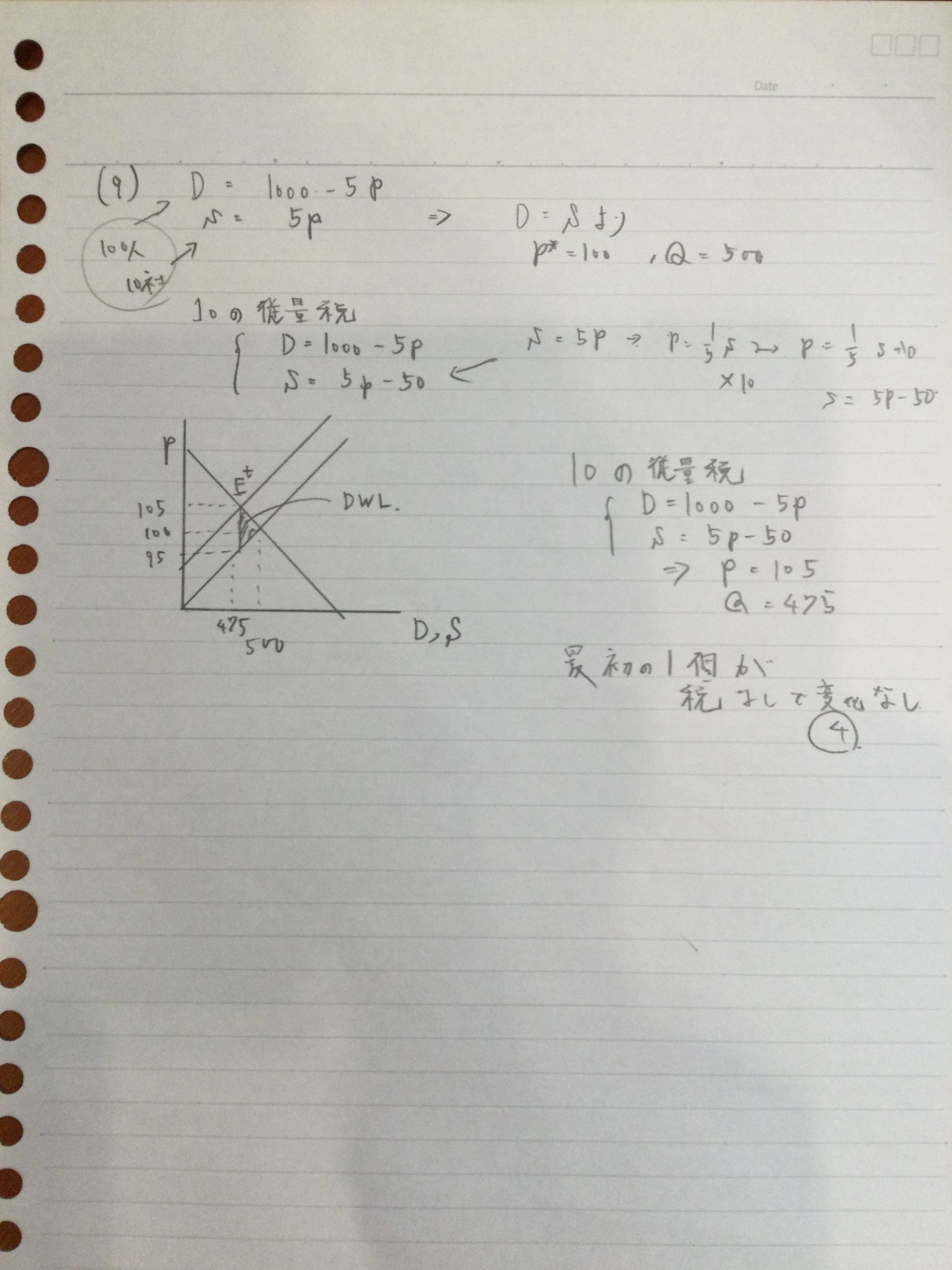
重量税、従価税、余剰、死荷重などをセットで覚えましょう。
(5)
クールノーの均衡。プレーヤーが2人の場合が定番ですが、それの拡張版での問題です。
(6)
それぞれの効用関数を実際に書いてみましょう。
(7)
予算制約を実際に書いてみましょう。
(8)
共同での利潤最大化を求めます。ピグー税がどの量になるか考えましょう。
(9)
(10)
(11)〜(15)
(16)〜(17)
(18)〜(20)
第2題
[1](1)〜(5)
[2](6)〜(10)