今回、テーマは医療経済学、情報の非対称性テーマになりました。
生活保護制度での医療扶助が過剰診療の原因になる可能性と、その対策について論じなさい。その際、以下の内容を含むこと。
(1)医療扶助の仕組みを公的医療保険の患者一部負担と比較する。また、医療扶助による患者負担を公的医療保険と違う仕組みとする意図を説明する。
(2)過剰診療が生じる理由を、モラルハザードに基づいて説明する。まずモラルハザードの意味を説明し、それが医療扶助でどのように働くかを説明する。また、医療サービスの需要曲線を示す図を用いる。
(3)モラルハザードによる過剰診療への対策を論じる。考えられる対策のデメリットも指摘する。
とあり、下記では主に
を解説します。問題に合わせてそれぞれまとめてみましょう。
また医療経済学の書籍、特に「健康経済学 — 市場と規制のあいだで 」でのモラルハザードのパートも読んでみましょう。
本書について
後藤
少子高齢化が進む日本で、医療や介護といった健康について関心が高まっています。とはいっても関連する財・サービスは、ドラッグストアで買うことができる一般薬のような市場で供給される財もありますし、規制の下で運営されている保険診療もあります。これをまとめて、消費者が真に求める「健康」の名を冠した経済学の教科書を書こうと共同執筆が始まりました。まず井深さんから、特に本書の執筆で力点を置いたところを教えていただきたいのですが。
井深
標準的な経済学のフレームワークを大事にしながら、実例の選択とかストーリーの構成において実際の医療制度や社会との関わりを重視した点だと思います。例えば、4章では需要の話で読者の普段の行動を考えながら読んで納得してもらえるような形になればと思っていました。
後藤
4章にはグロスマンモデルという健康需要の理論が出てきますがかなり抽象的です。
井深
個人の健康を希求する行動を効用最大化のフレームワークで説明した理論です。抽象化されているのはその通りなんですけれど、自分の身に置き換えながら考えることで、現実を考える場合に果たして理論が正しい角度で描写できているのかを考えるきっかけになるといいなと考えながら執筆しました。医療関係の方には少しとっつきにくい考え方だと思いますが、どうですか。
後藤
患者さんは医療サービスを求めているのではなくて、健康を求めているというのは当然ですし、予防医療などについても注目されていますので、消費者が健康を生産する側面を持つという考えも理解できるのではないかと思います。
井深
日頃医療者の方々は医療サービスの需要者である患者さんに接していらっしゃることが多いでしょうから、少し違う見方もできるかもしれないということを伝えることができれば本当にうれしいですね。
後藤
そうですね。逆に、グロスマンモデルのように健康や医療の経済分析に特徴的な理論を経済学部生に教えるときに難しさを感じたことはありますか?
井深
その辺が教える側の力量が問われているところだと思うのですが、経済学の教え方にこだわり過ぎると理論的な厳密性が中心になっていって、それを多種多様な存在から成り立つ現実とうまく絡めるというところが少し後回しになってしまうということがあるんですね。しかし、健康経済学という分野の場合、みんなの関心のある所は、もちろんモデルの面白さ自体に関心のある人も多いとは思うのですが、それ以外にこのモデルを使って何が考えられるのかな?とか、何が役に立つんだろう?というようなことだと思います。そういう部分を説明するためには、そのモデルが現実の保健医療とどういうふうに関わっているのかということを、制度との関係も含めて説明できるようにならないとなかなか面白さが伝わらないのかと思っています。ただ、そのバランスが難しいですね。
後藤
教える際の理論と実証のバランスの難しさというのは、非常に共感できると思います。一方で、どの現象に理論を当てはめようとするかで全く違いますが、理論自体の説明力に常に限界があります。例えば、グロスマンモデルのように動学的な意思決定として健康のことを長期的に考えられるような人は少ないかもしれませんね。このことに対して行動経済学の面から修正があったりなど研究も進んでいますね。
井深
経済学の中にもいろんな考え方があって、今の保健医療介護についてすべてを統一的に説明できるような理論はありません。でも、部分的にはかなりきっちり説明できるというようなバランスをどういうふうに読者に伝えていくかっていうのは本当に難しいですね。私は現在の政策においても重要な費用対効果の経済的基礎を扱った1章と効率と公正という公的制度の重要な問いを扱っている13章にも本書の特徴があると思います。
後藤
臨床をされている医療系の方にとっては、医療の費用対効果を医療経済学と考えておられる場合も少なくありません。諸外国で政策に用いられている費用対効果が、昨年度から日本でもと医療機器の価格を調整する際に明示的に考慮されるようになりました。こちらについても、経済学の理論的な背景をふまえながら、関係する医療制度全体の中でいろいろな政策の形がありうるということを説明するように心がけました。また、効率以外の要素については、13章で取り上げられていない考え方もたくさんあります。本書では、効率の視点と効率以外の視点を分けて議論することの重要性を強調しました。
後藤
この教科書では、標準的な経済学に依拠しつつも様々な考え方を紹介しています。一方で学生にとっては、多様な考え方が出てきてわけが分からなくなったりするというリスクもあると思います。教えられる際にはどのような工夫をなさいますか?
井深
そうですね。今仰ったように現実から物事を見ていくと、一つの視点だけで見るわけではないので、そういう意味ではグロスマンモデルみたいな形での一つの理論というのはそれだけで全ての現実を描写できていないというのはその通りだと思うんです。でも人々の選択の根拠を効用最大化という経済学の視点で考えることも重要なんだよということを説明して、ただ、それが保健医療介護を考える時の唯一の見方じゃないということもどこかで説明することが大事なのかな、と思います。
後藤
7章でとりあげた「供給者誘発「需要」も同様ですね。患者さんの健康改善を十分考えずに診療するお医者さんがいるのではないか、という問いから出発するというのは、医療界の人からはかなり違和感があることかもしれません。私は、医師に対する見方としてあり得るし、実際にも勤務先や働き方によって医師の行動原理はかなり変わると思っています。一方、医療系以外の学生に対しては、お医者さんへの理想と現実のバランスがあるという見方を持ってもらえるきっかけになればと考えています。
井深
そうですね。本の中でどの見方を説明するにも、なぜそのような見方が現実からみて理にかなっているのかという根拠を一生懸命書いたように記憶していますので、そういうところが伝わるといいな、と思います。
執筆の経緯について
井深
この本の執筆に至った経緯をもう一度振り返ってもよろしいですか。
後藤
私は現在ビジネススクールで教えているんですが、企業経営のミドル層・トップ層の方々にとって保健医療介護が、自分たちのビジネスを左右する可能性がある大きな経営環境として重要だということが共通認識になっていると思います。保健医療介護を考える際に経済学の視点で考えることは非常に重要だと思うのですが、一方で、「それは専門家の人たちが一生懸命考えていることだからその人たちに任せておけばいいことだ」と感じている印象も受けています。そこで、供給者目線、医療者目線の「医療経済学」ではなく、消費者目線の健康経済学の教科書を書きたいと考えました。
井深
これまでは健康を守るものすなわち医療という時代でしたから医療経済学と言う名前もしっくりしていたのですが、介護や保健も重要な時代になると状況は変わりますよね。
後藤
私自身も医療経済学という言葉の方が慣れていたのですが、だんだん健康経済学でないと違和感を覚えるようになるかもしれませんね。実は医療者側も、急性期医療に携わる方から介護や保健に関わる方まで本当に多様なので、より広い健康という概念を中心に経済学を学んでもらうのは有益だと思います。
井深
この本を書いていく中でいろいろな見方ができるということを再確認できて、この教科書を書きながら経済学が一つの物の見方だというような考え方を深められていったのではないかなと思います。読者の対象として、経済系の学生やビジネスパーソンだけではなく、医療系の学生や医療者の方々にも読んでいただきたいと考えていますので、幅広い視点で健康を考えて、消費者側・生産者側の立場を越えた議論につながるきっかけになればと思います。
この本の使い方について
後藤
医療系、経済系二つの読者層を想定していると言いましたが、医療者の方々には健康に関する財の取引も普通の経済活動とそんなに変わらない面も多いという見方を持ってほしいと思います。基本は変わらないけど、どの面は違うかっていう視点で考える、最初から医療が特別だというところから入らないでほしいなと思います。
井深
なるほど。私は経済学部を担当しているので主に経済学部の学生さんを念頭において考えますと、健康ってすごく身近な問題かつ社会にとっても重要な問題です。そういう問題を考える上でも経済学が有用な手段になるということが実感として伝わればいいなと思います。例えば、医療費の伸びの問題とかニュースで報道されることも多くて関心を持っている人も多いと思うんですが、そういう大きな問題の背景に個々の人がいて、医療を必要とする患者さんがいて、それを支える医療者がいて、またそれらを支える制度があって、ということを具体的に想像できるようになってほしいという願いを込めています。
後藤
研究者を目指す大学院生の方には何かメッセージはありますか?
井深
大学院生の方には、健康経済学を専門とする人は勿論、そうじゃない人にも手に取っていただけると嬉しいです。もともと健康経済学自体が労働経済学、財政学、産業組織論や人的資本を扱う教育の経済学と様々に相互関連を持っている分野なので、健康経済学という視点を通して自分の分野にも新しい発見があるかもしれません。
モラルハザード
下記はモラルハザードの典型的なケースを示している。
すべての個人が同一であり、病気にかかる確率 \( p \) に直面し、その病気が収入を減少させると仮定する。この場合の違いは、個人が病気の発生確率を低下させる予防措置 \( Z \) を取ることができることである。 \( dp/dZ < 0 \)とする。
\( \frac{dp}{dZ} < 0 \) の意味は、予防措置 \( Z \) を増やすと、病気にかかる確率 \( p \) が減少することを示している。具体的には、予防行動(例えば、健康的な食事をする、運動するなど)を増やすと、病気にかかる確率が低くなることを意味する。この関係を数学的に表現すると、予防行動 \( Z \) の増加に伴い、病気の確率 \( p \) が減少するので、その変化率 \( \frac{dp}{dZ} \) が負の値になるということである。 \( Z \) の価格は1とする。
保険会社は \( Z \) を観察することができない。彼らができることは、個人が \( P \) と \( X \) に応じて \( Z \) を調整することを知りながら、保険料 \( P \) と保険金 \( X \) を設定することだけである。
このモデルでは、期待効用の最大化は2つの段階で行われる。まず、個人は保険料 \( P \) と保険金 \( X \) を所与として、最適な \( Z \) の量を決定する。その後、保険会社は個人の \( Z \) の反応関数に基づいて、期待効用を最大化する \( P \) と \( X \) の金額を決定する。
最初に \( Z \) の決定を考える。
\[
\max_Z E(U) = (1 – p)U(Y – P – Z) + pU(Y – L – P – Z + X)
\]
一階条件は以下の通りである。
\[
\frac{\partial E(U)}{\partial Z} = – (1 – p)U'(H) – pU'(I) – U(H)\frac{\partial p}{\partial Z} + U(I)\frac{\partial p}{\partial Z} = 0
\]
ここで \( U(H) \) と \( U(I) \) はそれぞれ健康時と病気時の効用である。
項を整理すると、
\[
(1 – p)U'(H) + pU'(I) = (U(I) – U(H))\frac{\partial p}{\partial Z}
\]
となる。
左辺 (LHS) は期待限界効用の損失として表現される \( Z \) の限界費用である。右辺 (RHS) は期待効用の増加による \( Z \) の限界便益である。
次に、保険会社は \( P \) と \( Z \) が \( X \) の関数であると仮定して、保険金 \( X \) に関して \( E(U) \) を最大化する。自然な仮定として \( \partial Z/\partial X < 0 \) を導入する。個人は保険金が増えると予防活動を減らす。
モラルハザードの基礎は、個人が自分が被保険者の多くの一部であるため、 \( Z \) の変化が保険料に影響しないと仮定する一方で、予想される支払いは \( Z \) に依存するということである。
\[
\max_X E(U) = (1 – p)U(Y – P – Z) + pU(Y – L – P – Z + X)
\]
一階条件は以下の通りである。
\[
\frac{\partial E(U)}{\partial X} = pU'(I) – \frac{\partial P}{\partial X}[(1 – p)U'(H) + pU'(I)] – \frac{\partial Z}{\partial X}[(1 – p)U'(H) + pU'(I)] + \frac{\partial p}{\partial Z}\frac{\partial Z}{\partial X}[U(I) – U(H)] = 0
\]
(式3) から、最後の2つの項は0に等しい。したがって、
\[
\frac{\partial P}{\partial X}[(1 – p)U'(H) + pU'(I)] = pU'(I)
\]
移項して
\[
\frac{\partial P}{\partial X} = \frac{pU'(I)}{(1 – p)U'(H) + pU'(I)}
\]
となる。
(式7)の方程式は個人の予防活動の反応関数を考慮した保険契約の最適な限界価格スケジュールを示している。これは \( Z \) を観察できないため、第二の最良の最適解である。
保険会社が \( Z \) を観察できると仮定すると、第一段階で \( Z \) に依存する保険料を設定する。
\[
\max_Z E(U) = (1 – p)U(Y – P(Z) – Z) + pU(Y – L – P(Z) – Z + X)
\]
一階条件は次のように与えられる。
\[
-(1 – p)U'(H) \left[1 + \frac{\partial P}{\partial Z}\right] – pU'(I)\left[1 + \frac{\partial P}{\partial Z}\right] + (U(I) – U(H))\frac{\partial p}{\partial Z} = 0
\]
この条件での(式9)がゼロになるのは、次の場合である。
a. \( U(I) = U(H) \)、これは完全保険の場合に真である。
b. \( 1 + \frac{\partial P}{\partial Z} = 0 \)、これは \( Z \) の限界費用である。保険が実際に公平である場合、 \( P = pX \) となり、完全保険の下で \( P = pL \) となる。したがって、
\frac{\partial P}{\partial Z} = \frac{\partial p}{\partial Z}L
\]
これは期待損失の限界減少であり、 \( Z \) の限界便益である。個人は \( Z \) の限界便益がその限界費用と等しくなるように \( Z \) を購入する。実質的に、 \( Z \) を観察できることは \( p \) を観察できることに等しい。
ファーストベストの最適な解が得られ、個人にとってパレート最適な保険の量と最適な予防活動が得られる。これは、事前の状態が明らかになる前に予防活動を観察できれば、保険会社は最適なインセンティブを保ちながら最良の保険契約を提供できるという、保険文献の一般的な結果の特定の例である。
一方で、(式7) によるセカンドベスト(第二)の最良の最適解では、個人は \( Z \) を十分に行わないため、限界便益 (\( MB_Z \)) が限界費用 (\( MC_Z \)) より大きくなる。しかし、この差は \( Z \) を十分に購入しないことによって引き起こされる \( X \) の増加によって補償される (\( \frac{\partial Z}{\partial X} < 0 \))。保険会社の視点から見ると、 \( \frac{\partial P}{\partial X} \) が実際の請求額 \( X \) の限界変化と等しくなるようにしたい。
しかし、 \( Z \) を観察できないため、彼らができる最善のことは、限界価格スケジュールを予想される請求額または支払いの変化と等しくすることである。これを見るために、保険が実際に公平であると仮定し、 \( P = pX \) を再導入し、最大化において \( P \) を \( pX \) に置き換える。結果は次の通りである。
\[ p + \frac{\partial p}{\partial X} X = \frac{p U'(I)}{(1-p) U'(H) + p U'(I)} =\frac{\partial P}{\partial X}\]
と、なり
は、 \( X \) に関する予想支払いの変化である。
競争的なアウトカム
しかしながら、競争的な保険市場ではセカンドベスト(第二)の最良の価格スケジュールはほぼ確実に実現しない。その理由は以下の通りである。まず、保険会社はセカンドベスト(第二)の最良の価格スケジュールを実施するために、各個人が購入する保険の全量を把握する必要があるが、保険会社が知っているのは自社の保険契約者が購入した保険の量だけである。
次に、保険会社が購入された保険の量に応じて保険料を引き上げようとすると、被保険者はその会社から最初の単位の保険だけを購入し、追加の単位は他の会社から購入するだろう。最後に、競争企業は損益分岐点の条件に従う必要がある。すなわち、 \[ \sum_{i=1}^{N} P_i = \sum_{i=1}^{N} pX_i \] であり、ここで \(N\) は消費者数、保険が実際に公平であることを仮定する。すべての個人が同じリスク \(p\) を持つと仮定すると、保険の単位当たりの価格 \(p\) は \[ \frac{\sum_{i=1}^{N} pX_i}{\sum_{i=1}^{N} X_i} = p \] となり、すべての保険会社にとって同一である。なぜなら、彼らは価格受容者であるからである。 \( \frac{\partial P}{\partial X} = p \) となると、限界価格は \( p + \frac{\partial p}{\partial X} X \) のセカンドベスト(第二)の最良の最適水準よりも低くなり、被保険者は保険を過剰に購入する。実際、彼らは非常に多くの保険を購入する。 \( p = p \) である場合、(式7) は次のようになる。
または
(式12) は \( U(H) = U(I) \)、つまり完全保険を意味する。
さらに、\( Z = 0 \) となるのは(式3) から導かれる。完全保険では右辺 (RHS) がゼロであり、左辺 (LHS) は \( U'(H) > 0 \) である。 \( Z \) に対する支出は利益を伴わない効用の犠牲である。
直感的には、個人は価格(保険料)に影響を与えられないと仮定し、 \( p = p \) であるため、リスクを低減するインセンティブがない。競争的な保険の結果は、モラルハザードの存在下では非常に非効率的になり得る。
公共政策の対応
政府はおそらく、民間の保険会社と同様に個人の予防行動を観察することができない。
したがって、政府が個人の効用を最大化するためにできる最善の方法は、(式.10) によって示される第二の最良の結果を達成することである。
前述のように、第二の最良の限界価格スケジュール \( \frac{\partial P}{\partial X} \) を実施するには、各個人が購入する保険の総量を知る必要がある。
したがって、政府は個人に対して自分たちの保険購入総額を報告するよう求める必要がある。この要求が実行可能であると仮定すると、政府は(式7) に従って保険を提供することができる。
しかし、この点において、政府の提供には民間の保険会社に対する優位性はない。
なぜなら、各社が被保険者の総購入額を知っていれば、第二の最良の限界価格スケジュールを実施できるからである。
保険会社は、各 \( X \) の増分に対する保険料を、その \( X \) における予想される支払いの増分に基づいて設定する。同じ情報を持つすべての企業が同じ価格スケジュールを実施する。
個人は、最適な \( \frac{\partial P}{\partial X} \) 供給スケジュールの限界に基づいて購入を行い、市場は第二の最良の最適解で損益分岐点の均衡を達成するのである。
事後的モラルハザード
個人が支払いの確率に影響を与えられるというモラルハザードの古典的な定義は、事前的モラルハザードと呼ばれることが多い。
モラルハザードの定義は、医療が保険でカバーされているために実質的に低価格になり、医療を過剰に利用する結果も含むように拡大されている。
これが事後的モラルハザードと呼ばれる。2つのうち、事後的モラルハザードは医療市場において生じる非効率の量に関して間違いなく重要である。
不健康な生活習慣に従事することは、それ自体の直接的な効用コストを伴い、多くの人々がこれを避けることを選ぶ(これらのコストは、効用関数に健康を導入することで捉えることができる)。
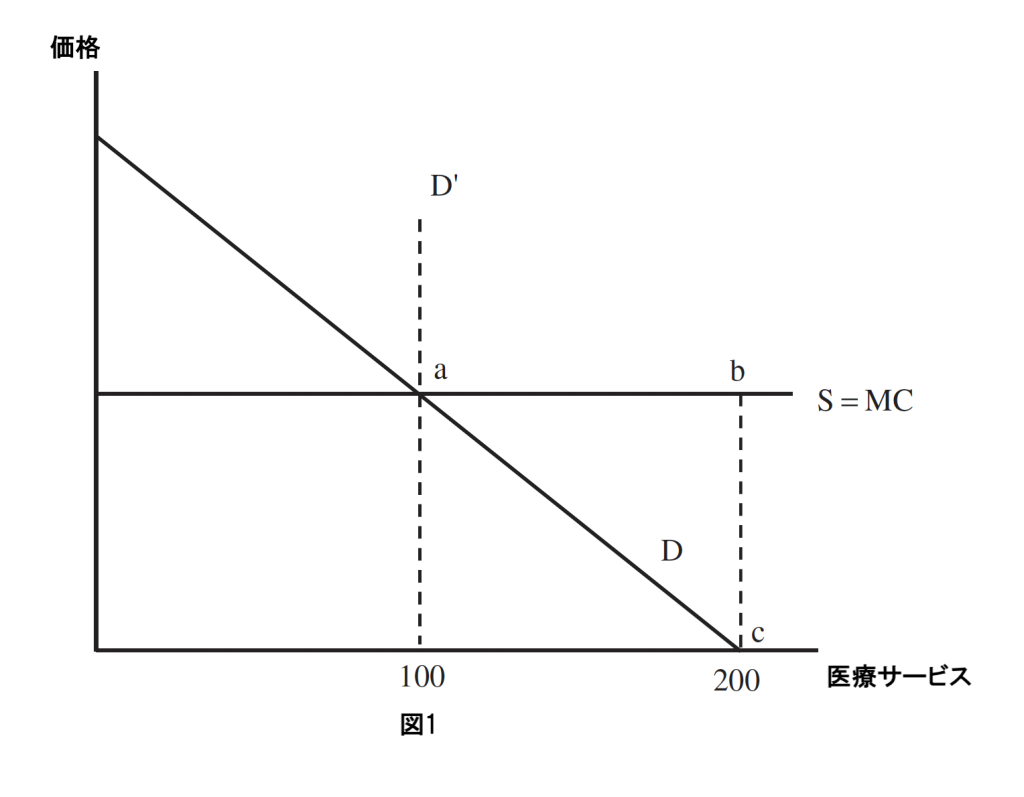
しかし、事後的モラルハザードは、図 1に示されるように、かなりの非効率を生み出す可能性がある。
横軸は医療の単位、縦軸はドルである。個人が病気になった場合の医療需要曲線をDとする。医療提供の限界費用はMCであり、供給曲線と仮定される。保険がない場合、個人はDとMCの交点で100単位の医療を購入する。病気になる確率は2分の1である。したがって、病気になることによる期待損失は0.5(100)MC = 50MCとなる。
医療需要曲線が完全に非弾性で100単位の医療を必要とする場合、個人が完全保険契約を受けると、保険料は50MCとなり、保険契約による期待支払いと等しくなり、個人の純収入は健康であろうと病気であろうとY – 50MCとなる。
リスク回避的な個人は、保険なしで50MCの期待損失に直面するよりも、確実に50MCを支払う方を好むだろう(これは、確定保険料と期待損失の関係でベルヌーイの定理を再述したものである)。
しかし、前述のD需要曲線のように、医療需要が弾力的であれば、完全保険の利点は明確ではない。問題は、完全保険下では医療を購入する際の限界費用がゼロであるため、被保険者が医療を過剰に利用し、図1では200単位の医療をゼロ価格で購入することである。
しかし、200単位の費用は200MCであり、保険会社はその費用を賄うために保険料を引き上げなければならない。保険料は100MC(= 0.5(200)MC)に上昇する。個人は、各状態で確実に100MCを犠牲にするよりも、50MCの期待損失に直面する方を好むかもしれない。
事後的モラルハザードの非効率性を理解する別の方法は、所得効果がないと仮定し、Dが実際の需要曲線であり補償された需要曲線でもあるとすることである。
保険を過剰に利用することによる個人の損失は、負の消費者余剰のabc領域であり、これは50から200単位までの医療を受ける追加的な150単位の価値に対する需要曲線の下の領域を差し引いた保険のコストに等しい。この損失は、完全保険が許す消費平準化の利益を上回る可能性がある。
実際、経験的な推定によれば、合理的なリスク回避の程度に対して、損失は消費平準化の利益を大幅に上回ることが示唆されている。
被保険者は囚人のジレンマに陥っている。パレート最適な結果は、各個人が完全保険を持ち、病気になった場合に100単位の医療を利用することである。
しかし、個人の視点からは、最善の行動は200単位をゼロ価格で購入し、その費用を他の全員に分担させることである。個人は、自分の行動がコストや保険料に目に見える影響を与えないと正しく仮定する。つまり、彼らは需要曲線の50から200単位までの領域を直接の利益として近視眼的に測定する。
しかし、全員がそのように考えるため、全員が200単位の医療を購入し、コストと保険料を引き上げ、非効率性を生み出し、保険の価値を損なう可能性がある 。
図1
控除額と共同支払い
民間および政府の保険会社が事後的モラルハザードを減少させるために一般的に採用する戦略は、控除額と共同支払いを要求することである。
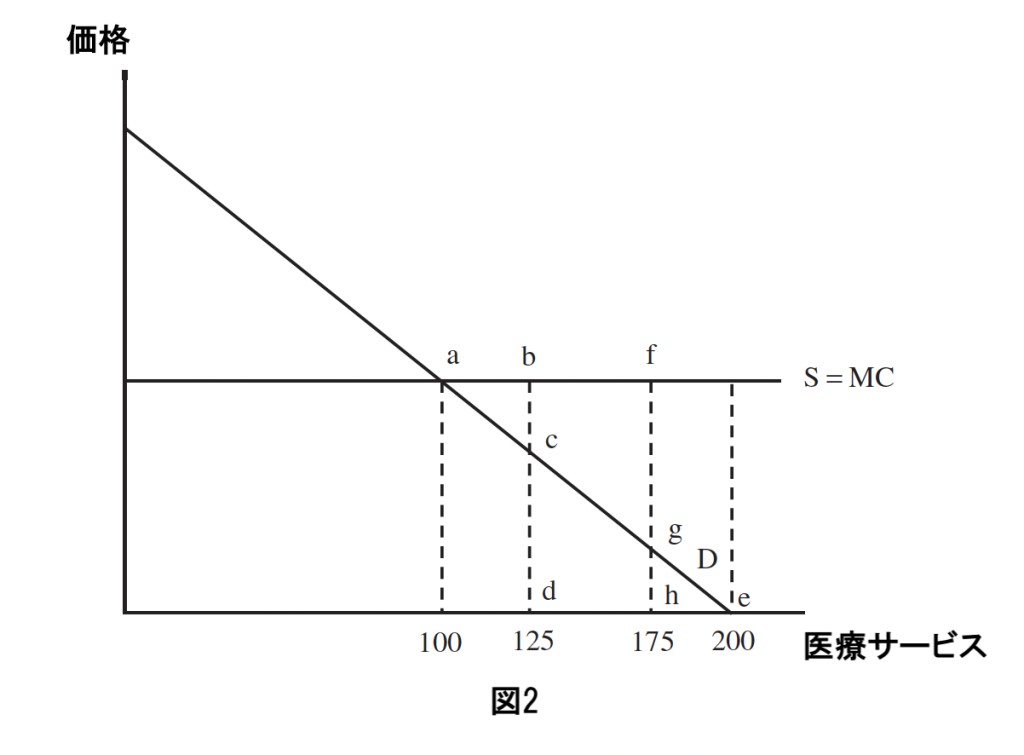
控除額が$Xである場合、被保険者は最初の$Xの医療費を自費で支払うことを意味する。控除額だけでは、少なくとも本モデルでは全く効果がないか、保険の需要を完全に取り除いてしまうかのどちらかである。図2を参照。
図2
被保険者が最初の125単位の医療費を自費で支払う控除額が設定された完全保険を受けると仮定する。控除額は、被保険者に対してabcの領域の費用を増加させ、これは100単位から125単位までの費用から、需要曲線の100単位から125単位の間の領域を差し引いたものである。
125単位から200単位までを無料で使用できることによる利益は、近視眼的にはcdeの領域、つまり125単位から200単位までの需要曲線の下の領域として見なされる。図のようにabc < cdeである場合、控除額は被保険者の行動に影響を与えない。
彼らは200単位を購入し続ける。しかし、控除額が十分に大きければ、例えば最初の175単位の控除額の場合、不等式が逆転する。被保険者に対する追加費用の領域afgが、175単位から200単位までを無料で使用できることによる追加利益の領域eghを上回り、個人は保険を購入しない。
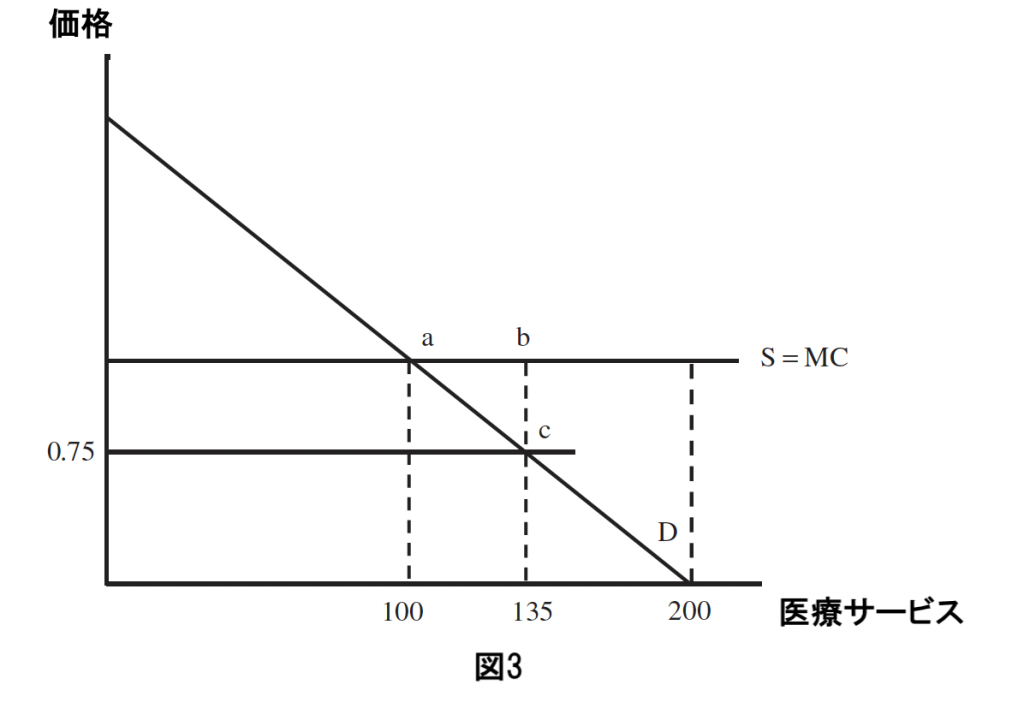
共同支払いはより有用である可能性がある。図3を参照。
被保険者が医療費の75%を支払う必要があると仮定する。図の横線0.75で示されている。この共同支払いにより、需要される医療の量は135単位に減少する。
被保険者にとっての純損失はabcの領域であり、これは135単位の医療をカバーする保険を持つことによる消費平準化の価値よりも少ないかもしれない。共同支払いは、完全保険下での見かけ上の価格がゼロである場合に、保険を過剰に利用するモラルハザードのインセンティブを減少させることで、保険を価値あるものにする可能性がある。
限界において、最適な共同支払い率は、過剰消費からくる非効率性を減らす利益と、医療費の支払いを増やすことによる消費平準化のコストのバランスを取るものである。
図3